1. Background
Electrocaloric effect is an adiabatic and reversible temperature change that occurs in a polar material due to the polarization change under an external electric field. Without applying an external electric field to a polar material, the dipole moments in the material are disordered, thus the total polarization vector is zero. When an electric field is applied, however, the dipoles are aligned along the electric field, the polarization is generated. During this process, the ordering of the dipoles increases in the material, which leads to a decrease of the material’s dipolar entropy. In an adiabatic condition, the lattice entropy will be increased since the total entropy keeps constant, and the electronic entropy could be neglected. As a result, the temperature of the material will be increased. This process is reversible due to the ergodicity of the thermodynamic properties of the material. Therefore, when the external electric field is removed the dipolar entropy increases, the lattice entropy declined, and the temperature of the material decreases in an adiabatic condition. If one isothermally combines the two processes between a load and an electrocaloric material by applying and removing an external electric field, the heat from the load will be transferred to the heat sink and the surrounding, and the load will be cooled. This is the principle of the cooling device using the ECE. The ECE is a solid-state cooling, which has lots of advantages, e.g., high energy conversion efficiency (>60% Carnot cycle), environmental friendliness.
The first experimental measurement on the ECE was carried out for Rochelle salt by Kobeko and Kurtschatov in 1930 [1]. But there was no ECE data reported in their research. In 1963, it was reexamined and an adiabatic temperature change of 0.0036 K was reported by Wisemann and Kuebler [2]. In 2006, a giant ECE was published by Mischenko et al. [3] in lead zirconate titanate thin films with an adiabatic temperature change of 12 K at 226 °C and 48 MV/m. In 2008, Neese et al. published a similar adiabatic temperature change of 12 K in P (VDF-TrFE) 55/45 mol % copolymers at 80 °C and 209 MV/m [4]. These two papers have triggered a revival of interest in the researches on ECE, and tremendous publications have come out, which refer to the theories and experiments of ECE in ferroelectric ceramics, single crystals, thin films, Langmuir-Blodgett films, polymers, liquid crystals, inorganic-organic composites etc [5-11] .
The aim of this review is to introduce the ECE and the phase transition in terms of the phenomenological theory for different ferroelectric materials. Through the introduction on the thermodynamic theory, we try to outline the guidelines to the research and development on ECE materials and devices.
2. Phenomenological theory
The application of Landau’s phenomenological theory for the ferroelectric phase transition in ferroelectrics was first carried out on barium titanate by Devonshire [12]. More recently it has been applied to the investigation of the ECE in various ferroelectric materials [13-16] . The elastic Gibbs free-energy for a stress free ferroelectric material can be expressed as a power series of polarization P
where T is the absolute temperature, T0 is the Curie-Weiss temperature and E is the external electric field. The parameters a0, b, c… etc. are called Landau phenomenological coefficients, which are usually assumed to be temperature independent. Here, we have assumed that the polarization and the electric field are uniaxial and orient in the same direction. At a given temperature and an external electric field, the stable phases and the corresponding polarization can be derived from the thermal equilibrium condition ∂G/∂P=0. Accordingly, the equilibrium state equation can be obtained from Equation 1,
Equation 2 implies the relationship between the polarization and temperature under various electric fields. Furthermore, differentiating E with respect to P yields the reciprocal of the permittivity
At zero field, E=0, the polarization is zero in the paraelectric state, thus the permittivity of paraelectric state can be expressed as
which obeys the Curie-Weiss law, εr=C/(T-T0). Hence, one can derived the coefficient a0 from fitting the experimental curve of permittivity above the transition temperature in ferroelectrics.
To investigate the ECE in ferroelectrics, one needs to calculate the
isothermal entropy change and the adiabatic temperature change due
to the phase transition. From the thermodynamic relation
and also the adiabatic temperature change (ΔT=-TΔS/CE) can be obtained
where CE is the heat capacity. The expression of the adiabatic temperature change indicates that ferroelectric materials with a large a0 and a large polarization under an external electric field would have a large ECE.
In addition, one can calculate the ECE based on the Maxwell relation
where ρ is the specific density. According to Equation 7 and 8, the expressions for the isothermal entropy change and the adiabatic temperature change of the electrocaloric material can be obtained
These two expressions show that the ECE can be determined from
the measurements of the temperature-dependent polarization under
various electric fields. This gives the theoretical basis of the well-known
indirect ECE measurement method which is widely used
in ECE measurements [3, 16-18]. In order to obtain large values of
isothermal entropy change and adiabatic temperature change, it
is required for electrocaloric material to possess large gradients of
polarization
3. ECE in first-order phase transition ferroelectrics
For a first-order phase transition, neglecting the higher terms, the elastic Gibbs free-energy can be expressed as
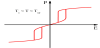
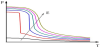
where a0, c>0 and b<0. The case of b <0 creates a first-order phase transition as shown in Figure 1. The free-energy plots of a firstorder transition are represented at three temperatures without an electric field. Tc is the transition temperature which is called Curie temperature. Below the transition temperature, the spontaneous polarization can be found and there exist local minima in the freeenergy at zero polarization. With the increasing temperature, the polarization changes from non-zero to zero discontinuously. Figure 2 shows the polarizations as a function of temperature under different electric fields. It can be found that a phase transition is induced by the applied electric field above the Curie temperature. By increasing the temperature, we may reach a point where the field-induced phase transition begins to disappear. The highest temperature that the electric field can induce phase transition is called critical temperature Tcp and the corresponding electric field is called critical electric field Ecp. Figure 3 shows the double hysteresis loop above Tc in a first-order phase transition material. When Tc< T< Tcp, a large enough electric field can induce the phase transition.
Since the discontinuous polarization occurs at the transition temperature, Equations 9 and 10 are not available for the first-order transition materials. The discontinuity of polarization will result in a latent heat and an entropy change. According to the Clausius- Clapeyron equation,
the expression of isothermal entropy change for first-order phase transition materials can be written as[19]
Equation 13 indicates that the polarization jump is in favor of the isothermal entropy change in first-order phase transition ferroelectrics. A larger isothermal entropy change of the system results in a larger adiabatic temperature change. Therefore, an ideal large ECE would be found in the first-order phase transition ferroelectric materials which have field-induced phase transition. The latent heat due to the filedinduced phase transition is ΔP∙ΔE/ΔT∙T.
4. ECE in second-order phase transition ferroelectrics
For a second-order phase transition, the sixth power term of the Gibbs free energy can be neglected, thus that
where both a0 and b are positive, and Tc is the Curie temperature, which is equal to the Curie-Weiss temperature. Figure 4 presents the schematic relationship between the free energy and the polarization under a zero electric field. This shows how the spontaneous polarization below the Curie temperature coincides with the zero polarization at Curie temperature. As shown in Figure 5, the spontaneous polarization decreases continuously to zero with the increase of temperature under a zero-field (black line). Unlike the first-order phase transition, there is no field-induced phase transition above Tc when an external electric field is applied on a second-order transition material. The equilibrium equation for a second-order phase transition can be written as
Substituting
where
5. ECE in relaxor ferroelectrics
In a relaxor ferroelectrics, the phase transition occurs in a broad temperature range unlike that in the normal ferroelectrics (firstorder or second-order phase transition) which occurs at certain temperature. Pirc et al. [7] presented a phenomenological theory model for relaxor ferroelectrics. A Landau-like Gibbs free-energy of a relaxor ferroelectric is expressed as
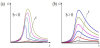
where coefficients a, b, c, …, etc. are temperature dependent. In normal ferroelectrics a is usually assumed as a=a0 (T-Tc ) and a0>0. Here, a(T)>0 at all temperatures and b can be either positive or negative. Figure 6 shows the temperature dependence of the polarization for the case of b < 0. When the electric field is large enough, a phase transition is induced which is similar to the case in a normal first-order phase transition material. This means that a field-induced first-order relaxor ferroelectric to normal ferroelectric phase transition occurs in relaxor until the electric field reaches the critical point ECP. Field-induced phase transition was experimentally confirmed in some relaxor ferroelectrics [8,17]. However, for the case of b < 0, the field-induced phase transition cannot be found.
The entropy of a relaxor ferroelectric includes the dipolar entropy (Sdip) and lattice entropy (Sph) which are dependent on the electric field. In adiabatic conditions, the total entropy change of system which passes from an initial state (E1, T1) to the final state (E2, T2) must be zero, hence we obtain
The change of lattice entropy can be expressed as
where Cph is the lattice heat capacity. Here, we assume that the change of Cph can be neglected in the temperature range near the phase transition. Combining Equations 18 and 19, setting the initial electric field E1 as zero and E2 written as E, we obtain
The dipolar entropy can be derived from the Equation 15 by Sdip=- (∂G⁄∂T)E
where a1=da/dT, b1=db/dT etc. As usual, assuming that b1, c1,… can be neglected, the change of dipolar entropy can be obtained
Substituting Equation 22 into Equation 18, one obtains
The ECE temperature change ΔT=T2-T1 at a given E and T (=T1) can be obtained by solving the Equation 23 by numerical algorithm. Because the argument of the exponential function is usually small, Equation 23 can be approximated as
Figure 7 shows the adiabatic temperature changes of a relaxor ferroelectric under different electric fields. For b < 0, near the fieldinduced phase transition temperature, there is a jump of ΔT and the jump disappears at the critical point. For b > 0, the ΔT is continue with the increasing temperature. Obviously, the ΔT shows a broad peak as a function of temperature near the transition temperature which is in qualitative agreement with the experiments [17,21].
6. Conclusions
This paper summarizes the phenomenological theory for ECE in first-order phase transition, second-order phase transition and relaxor ferroelectrics. External electric field can induce phase transition in the first-order phase transition materials and some relaxor (b < 0) ferroelectrics. The field-induced phase transition will lead to a latent heat which is an important part of the measured temperature change. Therefore, first-order transition and relaxor ferroelectrics would possess larger ECEs.
Competing Interests
The authors declare that they have no competing interests.