Profile

New User

New to Graphy Publications? Create an account to get started today.

Registered Users

Have an account? Sign in now.

How to Cite | Author Information | Publication History | Funding Information
International Journal of Metallurgical & Materials Engineering Volume 4 (2018), Article ID 4:IJMME-141, 5 pages
http://dx.doi.org/10.15344/2455-2372/2018/141
Review Article
Electrocaloric Effect and Phase Transitions in Ferroelectrics

Dandan Li and Sheng-Guo Lu*

School of Materials and Energy,Guangdong University of Technology, Guangzhou, 510006 China
Prof. Sheng-Guo Lu, Guangdong Provincial Research Center on Smart Materials and Energy Conversion Devices, Guangdong Provincial Key Laboratory of Functional Soft Condensed Matter, School of Materials and Energy,Guangdong University of Technology, Guangzhou, 510006 China; E-mail: sglu@gdut.edu.cn
04 March 2018; 21 April 2018; 23 April 2018
Li D, Lu SG (2018) Electrocaloric Effect and Phase Transitions in Ferroelectrics. Int J Metall Mater Eng 4: 141. doi: https://doi.org/10.15344/2455-2372/2018/141
This work was supported by the Natural Science Foundation of China (Grant No. 51372042), the Guangdong Provincial Natural Science Foundation (2015A030308004), and the NSFC-Guangdong Joint Fund (Grant No. U1501246).
© 2018 Li et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Abstract

This review summarizes the electrocaloric effect (ECE) and phase transition in terms of the phenomenological theory of ferroelectric materials. Field-induced phase transition can happen in firstorder phase transition materials and some relaxor ferroelectrics under a high enough electric field. The adiabatic temperature change ΔT under a given electric field shows a peak at the ferroelectricparaelectric transition which is agreement with the experimental results. The first-order transition and relaxor ferroelectrics would possess larger ECEs than that in a second-order transition ferroelectrics due to the jump of polarization. This relationship between the phase transition and the electrocaloric effect may be helpful in developing new materials for electrocaloric applications.


1. Background

Electrocaloric effect is an adiabatic and reversible temperature change that occurs in a polar material due to the polarization change under an external electric field. Without applying an external electric field to a polar material, the dipole moments in the material are disordered, thus the total polarization vector is zero. When an electric field is applied, however, the dipoles are aligned along the electric field, the polarization is generated. During this process, the ordering of the dipoles increases in the material, which leads to a decrease of the material’s dipolar entropy. In an adiabatic condition, the lattice entropy will be increased since the total entropy keeps constant, and the electronic entropy could be neglected. As a result, the temperature of the material will be increased. This process is reversible due to the ergodicity of the thermodynamic properties of the material. Therefore, when the external electric field is removed the dipolar entropy increases, the lattice entropy declined, and the temperature of the material decreases in an adiabatic condition. If one isothermally combines the two processes between a load and an electrocaloric material by applying and removing an external electric field, the heat from the load will be transferred to the heat sink and the surrounding, and the load will be cooled. This is the principle of the cooling device using the ECE. The ECE is a solid-state cooling, which has lots of advantages, e.g., high energy conversion efficiency (>60% Carnot cycle), environmental friendliness.

The first experimental measurement on the ECE was carried out for Rochelle salt by Kobeko and Kurtschatov in 1930 [1]. But there was no ECE data reported in their research. In 1963, it was reexamined and an adiabatic temperature change of 0.0036 K was reported by Wisemann and Kuebler [2]. In 2006, a giant ECE was published by Mischenko et al. [3] in lead zirconate titanate thin films with an adiabatic temperature change of 12 K at 226 °C and 48 MV/m. In 2008, Neese et al. published a similar adiabatic temperature change of 12 K in P (VDF-TrFE) 55/45 mol % copolymers at 80 °C and 209 MV/m [4]. These two papers have triggered a revival of interest in the researches on ECE, and tremendous publications have come out, which refer to the theories and experiments of ECE in ferroelectric ceramics, single crystals, thin films, Langmuir-Blodgett films, polymers, liquid crystals, inorganic-organic composites etc [5-11] .

The aim of this review is to introduce the ECE and the phase transition in terms of the phenomenological theory for different ferroelectric materials. Through the introduction on the thermodynamic theory, we try to outline the guidelines to the research and development on ECE materials and devices.

2. Phenomenological theory

The application of Landau’s phenomenological theory for the ferroelectric phase transition in ferroelectrics was first carried out on barium titanate by Devonshire [12]. More recently it has been applied to the investigation of the ECE in various ferroelectric materials [13-16] . The elastic Gibbs free-energy for a stress free ferroelectric material can be expressed as a power series of polarization P

G= G 0 + 1 2 a 0 ( T− T 0 ) P 2 + 1 4 b P 4 + 1 6 c P 6 +…−EP

where T is the absolute temperature, T0 is the Curie-Weiss temperature and E is the external electric field. The parameters a0, b, c… etc. are called Landau phenomenological coefficients, which are usually assumed to be temperature independent. Here, we have assumed that the polarization and the electric field are uniaxial and orient in the same direction. At a given temperature and an external electric field, the stable phases and the corresponding polarization can be derived from the thermal equilibrium condition ∂G/∂P=0. Accordingly, the equilibrium state equation can be obtained from Equation 1,

E= a 0 ( T− T 0 )P+b P 3 +c P 5 +…

Equation 2 implies the relationship between the polarization and temperature under various electric fields. Furthermore, differentiating E with respect to P yields the reciprocal of the permittivity

1 ε = ∂E ∂P = a 0 ( T− T 0 )+3b P 2 +5c P 4 +…

At zero field, E=0, the polarization is zero in the paraelectric state, thus the permittivity of paraelectric state can be expressed as

ε= 1 a 0 ( T− T 0 )

which obeys the Curie-Weiss law, εr=C/(T-T0). Hence, one can derived the coefficient a0 from fitting the experimental curve of permittivity above the transition temperature in ferroelectrics.

To investigate the ECE in ferroelectrics, one needs to calculate the isothermal entropy change and the adiabatic temperature change due to the phase transition. From the thermodynamic relation ΔS=− ( ∂G ∂T ) P , the isothermal entropy change can be derived from Equation 1

ΔS=− 1 2 a 0 P 2

and also the adiabatic temperature change (ΔT=-TΔS/CE) can be obtained

ΔT= T 2 C E a 0 P 2

where CE is the heat capacity. The expression of the adiabatic temperature change indicates that ferroelectric materials with a large a0 and a large polarization under an external electric field would have a large ECE.

In addition, one can calculate the ECE based on the Maxwell relation

( ∂T ∂E ) T = ( ∂P ∂T ) E

( ∂T ∂E ) S =− T ρ C E ( ∂P ∂T ) E

where ρ is the specific density. According to Equation 7 and 8, the expressions for the isothermal entropy change and the adiabatic temperature change of the electrocaloric material can be obtained

ΔS= ∫ E 1 E 2 ( ∂P ∂T ) E dE

ΔT=− ∫ E 1 E 2 T ρ C E ( ∂P ∂T ) E dE

These two expressions show that the ECE can be determined from the measurements of the temperature-dependent polarization under various electric fields. This gives the theoretical basis of the well-known indirect ECE measurement method which is widely used in ECE measurements [3, 16-18]. In order to obtain large values of isothermal entropy change and adiabatic temperature change, it is required for electrocaloric material to possess large gradients of polarization ( ∂P ∂T ) E and large breakdown-with stand fields.

3. ECE in first-order phase transition ferroelectrics

For a first-order phase transition, neglecting the higher terms, the elastic Gibbs free-energy can be expressed as

G= G 0 + 1 2 a 0 ( T− T 0 ) P 2 + 1 4 b P 4 + 1 6 c P 6 −EP

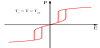
where a0, c>0 and b<0. The case of b <0 creates a first-order phase transition as shown in Figure 1. The free-energy plots of a firstorder transition are represented at three temperatures without an electric field. Tc is the transition temperature which is called Curie temperature. Below the transition temperature, the spontaneous polarization can be found and there exist local minima in the freeenergy at zero polarization. With the increasing temperature, the polarization changes from non-zero to zero discontinuously. Figure 2 shows the polarizations as a function of temperature under different electric fields. It can be found that a phase transition is induced by the applied electric field above the Curie temperature. By increasing the temperature, we may reach a point where the field-induced phase transition begins to disappear. The highest temperature that the electric field can induce phase transition is called critical temperature Tcp and the corresponding electric field is called critical electric field Ecp. Figure 3 shows the double hysteresis loop above Tc in a first-order phase transition material. When Tc< T< Tcp, a large enough electric field can induce the phase transition.

figure 1
Figure 1: Schematic relationship between free energy and polarization of a first-order transition at three different temperatures.
figure 2
Figure 2: Temperature-dependent polarization of first-order phase transition under different electric fields.
figure 3
Figure 3: Double hysteresis loop above transition temperature in firstorder transition materials.

Since the discontinuous polarization occurs at the transition temperature, Equations 9 and 10 are not available for the first-order transition materials. The discontinuity of polarization will result in a latent heat and an entropy change. According to the Clausius- Clapeyron equation,

ΔT ΔE = ΔP ΔS

the expression of isothermal entropy change for first-order phase transition materials can be written as[19]

ΔS= ∫ E 1 E 2 ( ∂P ∂T ) E dE+ΔP( ΔE ΔT )

Equation 13 indicates that the polarization jump is in favor of the isothermal entropy change in first-order phase transition ferroelectrics. A larger isothermal entropy change of the system results in a larger adiabatic temperature change. Therefore, an ideal large ECE would be found in the first-order phase transition ferroelectric materials which have field-induced phase transition. The latent heat due to the filedinduced phase transition is ΔP∙ΔE/ΔT∙T.

4. ECE in second-order phase transition ferroelectrics

For a second-order phase transition, the sixth power term of the Gibbs free energy can be neglected, thus that

G= G 0 + 1 2 a 0 ( T− T c ) P 2 + 1 4 b P 4 −EP

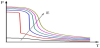
where both a0 and b are positive, and Tc is the Curie temperature, which is equal to the Curie-Weiss temperature. Figure 4 presents the schematic relationship between the free energy and the polarization under a zero electric field. This shows how the spontaneous polarization below the Curie temperature coincides with the zero polarization at Curie temperature. As shown in Figure 5, the spontaneous polarization decreases continuously to zero with the increase of temperature under a zero-field (black line). Unlike the first-order phase transition, there is no field-induced phase transition above Tc when an external electric field is applied on a second-order transition material. The equilibrium equation for a second-order phase transition can be written as

figure 4
Figure 4: Schematic relationship between free energy and polarization of a second-order transition at three different temperatures.
figure 5
Figure 5: Temperature-dependent polarization of second-order phase transition under different electric fields.

E= a 0 ( T− T c )P+b P 3

Substituting ΔT= T 2 C E a 0 P 2 into Equation 15, the relation between the adiabatic temperature change and the electric field can be obtained

E= a k 1/2 Δ T 1/2 + b k 3/2 Δ T 3/2

where k= a 0 T 2 C E and a=a0 (T-T0 ). Equation (16) is the modified Belov-Goryaga equation for ECE in a second-order phase transition material proposed by Lu et al. [20] in 2012. It indicates that ΔT depends on E2 at lower electric fields and on E(2/3) at higher electric fields. It should be noted that the modified Belov-Goryaga equation is derived from the phenomenological theory of second-order phase transition. For the first-order transition, the similar equation could be derived, but the sixth power term of polarization should be taken into account.

5. ECE in relaxor ferroelectrics

In a relaxor ferroelectrics, the phase transition occurs in a broad temperature range unlike that in the normal ferroelectrics (firstorder or second-order phase transition) which occurs at certain temperature. Pirc et al. [7] presented a phenomenological theory model for relaxor ferroelectrics. A Landau-like Gibbs free-energy of a relaxor ferroelectric is expressed as

G= G 0 + 1 2 a P 2 + 1 4 b P 4 + 1 6 c P 6 +…−EP

where coefficients a, b, c, …, etc. are temperature dependent. In normal ferroelectrics a is usually assumed as a=a0 (T-Tc ) and a0>0. Here, a(T)>0 at all temperatures and b can be either positive or negative. Figure 6 shows the temperature dependence of the polarization for the case of b < 0. When the electric field is large enough, a phase transition is induced which is similar to the case in a normal first-order phase transition material. This means that a field-induced first-order relaxor ferroelectric to normal ferroelectric phase transition occurs in relaxor until the electric field reaches the critical point ECP. Field-induced phase transition was experimentally confirmed in some relaxor ferroelectrics [8,17]. However, for the case of b < 0, the field-induced phase transition cannot be found.

figure 6
Figure 6: Temperature-dependent polarization of relaxor ferroelectrics with b < 0 under different electric fields.

The entropy of a relaxor ferroelectric includes the dipolar entropy (Sdip) and lattice entropy (Sph) which are dependent on the electric field. In adiabatic conditions, the total entropy change of system which passes from an initial state (E1, T1) to the final state (E2, T2) must be zero, hence we obtain

S ph ( T 2 )− S ph ( T 1 )=−[ S dip ( E 2 , T 2 )− S dip ( E 1 , T 1 ) ]

The change of lattice entropy can be expressed as

S ph ( T 2 )− S ph ( T 1 )= ∫ T 1 T 2 C ph T dT≅ C ph ln( T 2 T 1 )

where Cph is the lattice heat capacity. Here, we assume that the change of Cph can be neglected in the temperature range near the phase transition. Combining Equations 18 and 19, setting the initial electric field E1 as zero and E2 written as E, we obtain

T 2 = T 1 exp{ − 1 C ph [ S dip ( E, T 2 )− S dip ( 0, T 1 ) ] }

The dipolar entropy can be derived from the Equation 15 by Sdip=- (∂G⁄∂T)E

S dip =− ( ∂ G 0 ∂T ) E −( 1 2 a 1 P 2 + 1 4 b 1 P 4 + 1 6 c 1 P 6 +… )

where a1=da/dT, b1=db/dT etc. As usual, assuming that b1, c1,… can be neglected, the change of dipolar entropy can be obtained

S dip ( E, T 2 )− S dip ( 0, T 1 )= 1 2 a 1 ( T 1 ) P 2 ( 0, T 1 )− 1 2 a 1 ( T 2 ) P 2 ( E, T 2 )

Substituting Equation 22 into Equation 18, one obtains

T 2 = T 1 exp{ 1 2 C ph [ a 1 ( T 2 ) P 2 ( E, T 2 )− a 1 ( T 1 ) P 2 ( 0, T 1 ) ] }

The ECE temperature change ΔT=T2-T1 at a given E and T (=T1) can be obtained by solving the Equation 23 by numerical algorithm. Because the argument of the exponential function is usually small, Equation 23 can be approximated as

ΔT= T 2 C ph [ a 1 ( T+ΔT ) P 2 ( E,T+ΔT )− a 1 ( T 1 ) P 2 ( 0,T ) ]

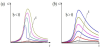
Figure 7 shows the adiabatic temperature changes of a relaxor ferroelectric under different electric fields. For b < 0, near the fieldinduced phase transition temperature, there is a jump of ΔT and the jump disappears at the critical point. For b > 0, the ΔT is continue with the increasing temperature. Obviously, the ΔT shows a broad peak as a function of temperature near the transition temperature which is in qualitative agreement with the experiments [17,21].

figure 7
Figure 7: Adiabatic temperature changes of a relaxor with (a) b < 0 and (b) b > 0 under different electric fields.

6. Conclusions

This paper summarizes the phenomenological theory for ECE in first-order phase transition, second-order phase transition and relaxor ferroelectrics. External electric field can induce phase transition in the first-order phase transition materials and some relaxor (b < 0) ferroelectrics. The field-induced phase transition will lead to a latent heat which is an important part of the measured temperature change. Therefore, first-order transition and relaxor ferroelectrics would possess larger ECEs.

Competing Interests

The authors declare that they have no competing interests.


References

  1. Kobeko P, Kurchatov I (1930) Dielectric properties of ferroelectrics. Zeitschrift für Physik 66: 192-205.
  2. Wisemann GG, Kuebler JK (1963) Electrocaloric effect in ferroelectric Rochelle salt. Physics Review 131: 2023-2027. View
  3. Mischenko AS, Zhang QM, Scott J, Whatmore RW, Mathur ND, et al. (2006) Giant Electrocaloric Effect in Thin-film PbZr0.95Ti0.05O3. Science 311: 1270-1271. View
  4. Neese B, Chu B, Lu SG, Wang Y, Furman E, et al. (2008) Large Electrocaloric Effect in Ferroelectric Polymers Near Room Temperature. Science 321: 821-823. View
  5. Lu SG, Neese B, Chu BJ, Wang Y, Zhang QM, et al. (2008) Large electric tunability in poly(vinylidene fluoride-trifluoroethylene) based polymers. Appl Phys Lett 93: 42905. View
  6. Lu SG, Zhang QM (2009) Electrocaloric Materials for Solid-State Refrigeration. Adv Mater 21: 1983-1987. View
  7. Pirc R, Kutnjak Z, Blinc R, Zhang QM (2011) Electrocaloric effect in relaxor ferroelectrics. J Appl Phys 110: 741137. View
  8. Colla EV, Jurik N, Liu YH, Delgado MEX, Weissman MB, et al. (2013) Kinetics and thermodynamics of the ferroelectric transitions in PbMg1/3Nb2/3O3 and PbMg1/3Nb2/3O3-12% PbTiO3 crystals. J Appl Phys 113: 184104. View
  9. Heitmann AA, Rossetti GA (2014) Thermodynamics of Ferroelectric Solid Solutions with Morphotropic Phase Boundaries. J Am Ceram Soc 97: 1661- 1685. View
  10. Qian XS, Ye HJ, Zhang YT, Gu HM, Y LX, et al. (2014) Giant Electrocaloric Response Over A Broad Temperature Range in Modifi ed BaTiO3 Ceramics. Adv Funct Mater 24: 1300-1305. View
  11. Lu XY, Zheng LM, Li H, Cao WW (2015) Theoretical study on phase coexistence in ferroelectric solid solutions near the tricritical point. J Appl Phys 117: 134101. View
  12. Devonshire AF (1954) Theory of Ferroelectrics. Adv Phys 3: 85-130. View
  13. Rozic B, Kosec M, Ursic H, Holc H, Malic B, et al. (2011) Influence of the critical point on the electrocaloric response of relaxor ferroelectrics. J Appl Phys 110: 641186. View
  14. Liu Y, Wei J, Janolin P, Infante I, Kreisel J, et al. (2014) Prediction of giant elastocaloric strength and stress-mediated electrocaloric effect in BaTiO3 single crystals. Phys Rev B 90: 104101-104107. View
  15. Wu HH, Zhu J, Zhang TY (2015) Double hysteresis loops and large negative and positive electrocaloric effects in tetragonal ferroelectrics. Phys Chem Chem Phys 17: 23897. View
  16. Wu HH, Zhu J, Zhang TY (2015) Pseudo-first-order phase transition for ultrahigh positive/negative electrocaloric effects in perovskite ferroelectrics. Nano Energy 16: 419-426. View
  17. Peräntie J, Hagberg J, Uusimäki A, Jantunen H (2010) Electric-field-induced dielectric and temperature changes in a <011>-oriented Pb(Mg1/3Nb2/3)O3- PbTiO3 single crystal. PHYSICAL REVIEW B 82: 134119. View
  18. Geng W, Liu Y, Meng X, Bellaiche L, Scott JF, et al. (2015) Giant Negative Electrocaloric Effect in Antiferroelectric La-Doped Pb(ZrTi)O3 Thin Films Near Room Temperature. Adv Mater 27: 3165-3169. View
  19. Lu SG, Tang XG, Wu SH, Zhang QM (2014) Large Electrocaloric Effect in Ferroelectric Materials. J Inorg Mater 29: 6-12. View
  20. Lu SG, Rozic B, Zhang QM, Kutnjak Z, Pirc R, et al. (2012) Electrocaloric effect in ferroelectric polymers. Appl Phys A-Mater 107: 559-566. View
  21. Luo L, Dietze M, Solterbeck C, Es-Souni M, Luo H, et al. (2012) Orientation and phase transition dependence of the electrocaloric effect in 0.71PbMg1/3Nb2/3O3-0.29PbTiO3 single crystal. Appl Phys Lett 101: 62907. View
Best viewed in Mozilla Firefox, Google Chrome, Safari, Above IE 9.0 version
Privacy Policy | Copyright & Permissions
Copyright © 2013-2024 Graphy Publications, All Rights Reserved.