Profile

New User

New to Graphy Publications? Create an account to get started today.

Registered Users

Have an account? Sign in now.

How to Cite | Author Information | Publication History
International Journal of Diabetes & Clinical Diagnosis Volume 3 (2016), Article ID 3:IJDCD-116, 6 pages
http://dx.doi.org/10.15344/2394-1499/2016/116
Review Article
System Engineering Approach of Diabetes Treatment

Levente Kov´acs*, Gy¨orgy Eigner

John von Neumann, Faculty of Informatics, University Research and Innovation Center, Physiological Controls Group, Obuda University, Budapest, Hungary
Dr. Levente Kov´acs, John von Neumann, Faculty of Informatics, University Research and Innovation Center, Physiological Controls Group, Obuda University, Budapest, Hungary; E-mail: kovacs.levente@nik.uni-obuda.hu
31 October 2015; 16 April 2016; 18 April 2016
Kov´acs L, Eigner G (2016) System Engineering Approach of Diabetes Treatment. Int J Diabetes Clin Diagn 3: 116. doi: http://dx.doi.org/10.15344/2394-1499/2016/116
© 2016 Kov´acs et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Abstract

The paper gives a short system engineering review on the treatment of diabetes covering control engineering and mathematical modeling issues. The Artificial Pancreas (AP) concept is discussed together with the Intensive Care (ICU) idea for automatic treatment of diabetic patients. This highly interdisciplinary concept involves beyond medical sciences, control engineering and biomedical engineering knowledge. Having already developed continuous glucose sensor devices and highly performant insulin pumps, the automatic control concept could be an efficient solution for millions of people living with diabetes for accurate metabolic conditions management.


1. Introduction

Diabetes Mellitus (DM) or shortly diabetes is used as the collective name of several chronic metabolic diseases of the human body where by impaired insulin production the human body cannot automatically regulate the glucose level [1,2]. Different types of DM exist associated with diverse symptoms and side effects. The main types are the following [3]:

  1. Type 1 or insulin-dependent DM (T1DM);
  2. Type 2 or insulin-independent DM (T2DM);
  3. Gestational DM (GDM);
  4. Double DM (DDM);
  5. Genetic related DM (GrDM);
  6. Other types of DM which can be induced by different kind of diseases, drugs, chemicals and cancers [3].

Type 1 and type 2 cover more than 95% of the cases, T1DM being more critical. T1DM is an autoimmune disease, which mainly appears in young age and its general medical symptom can be described by the fact that the immune system of human body automatically destroys the beta-cells responsible for insulin production. As a result, in case of T1DM the patient needs immediate insulin treatment to avoid the metabolic breakdown, which starts with hypoglycemic and ketoacidotic state and ends with the death of the patient [2,4]. This is the fact why T1DM is known as insulin dependent DM.

T2DM is the ’Civilization Disease’ form of DM as it is largely related to the wrong or not appropriate nourishment [5]. T2DM is a self-generating process which appears after long term hyperglycemia slowly increasing insulin insensitivity during the years. No insulin injection is needed at the beginning of this type of DM, but in its final un- or poorly-treated stage it needs continuous external insulin treatment to handle the level of glycemia [6,7]. In case of DDM the worst effects of T1DM and T2DM prevail, namely, the autoimmune effects are coupled with increasing insulin resistance. This type of DM has upward prevalence in the recent years, which caused by the double metabolic stress comes from genetic predisposition and lifestyle [8-10].

GDM occurs during pregnancy and most of the cases the DM state ends with the birth, however, those women who suffer from GDM particularly are inclined to emergence of other type of DM in their later life [11,12]. Genetic and the other types of DM can be caused by several disorders [3]. Unfortunately, the occurrence of DM shows an increasing trend. According to the World Health Organization’s study diabetic population will be doubled from 2000 to 2030 exceeding 366 million people [13]. Newer studies have reported that this number is already exceeded and the total count of the diabetic population was around 382 million in 2013, worldwide. Moreover, the projected number of diagnosed and undiagnosed DM cases is going to reach 592 million in 2035 which is the 4.8-6.1% of the estimated total human population on Earth [1,14].

Although DM is still incurable, the therapy of DM presented considerable progression in the recent years, for instance the appearance of different cell stimulating drugs [7,15], partial immunosuppressant drug applications in order to reduce the autoimmune effect [16], transplantation of Langerhansislets [17] or pancreas [18] and stem cell experiments [17] are just some of the achieved results.

The regular treatment for a diabetic patient on insulin treatment is based on external insulin injections. There are two main directions for the insulin administration:

  • Insulin administration with insulin pens, which represents the ordinary, conservative therapy;
  • Insulin administration with insulin pumps, which is a highly developed electromechanical device.

Both methods have the same purposes from a diabetic patient point of view: keeping the blood sugar level in a narrow, normoglycemic range (3.9-6 mmol/L or 70-110 mg/dL). An important part of these therapies relies on reaching different quality requirements, like body weight, level of physical activation and levels of physiological markers. The main difference is the way how these requirements are achieved. By the appearance of the insulin pump therapy the automated treatment possibility of diabetic patients has created known as the Artificial Pancreas (AP) concept. AP represents today the most challenging engineering tool in the treatment of DM [19]. In the following section, we summarize the AP concept, realization tools and devices, and the engineering considerations behind.

2. Discussion

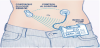
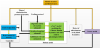
2.1 The concept of Artificial Pancreas In order to realize an AP three necessary subparts is needed [19-21]:

  1. An insulin pump that stores and injects the rapid acting insulin;
  2. A Continuous Glucose Monitoring System (CGMS) for continuous blood sugar level measurement;
  3. Appropriate software components including control algorithms, user interfaces, drivers.

Several insulin pumps are available on the global market [22-24] with different solutions. The basic concept is an ’All-in-One’ type device, where the hardware, mechanical and software subparts are integrated into one device [25]. The other conceptual realization is the divided solution, where important subsystems like the control algorithm or raw data processing are running on an additional device [26,27]. The insulin pump contains an insulin cartridge, a Graphical User Interface (GUI), the battery and the necessary mechanical and hardware elements to inject the insulin and to operate the device. The CGMS system is used in parallel with the insulin pump. The operations of CGMS are based on various principles.

In practice, the most widely used systems are external devices fixed on the abdominal skin surface and connected to the subcutaneous level through a thin catheter. The most frequent measuring principles are enzymatic based (Glucose Oxidase (GOx)). Beside its several benefits CGMS has also some disadvantages mostly from control engineering point of view: sensors measurements are done only every 5 minutes. Implantable CMGS have been also appeared, but these are not available on the market, yet [28].

As mentioned above, the third necessary component to realize the AP is the appropriate software elements, including the control algorithms, the ”soul” of this approach. Figure 1 shows the schematic representation of the AP concept.

figure 1
Figure 1: General concept of the AP[29].

2.2 Control Algorithms for AP

Due to the fact that insulin pump therapies are used mostly in case of T1DM, the advanced control algorithms developed inside AP researches focus on this DM form. The main expectation from an AP control algorithm is the automatic glucose regulation in order to keep the blood glucose concentration in the normal glycemic range, i.e. 70- 110 mg/dL (3.9-6 mmol/L) and relying if possible on the compliance of the patient. The ultimate goal is to avoid the dangerously low blood glucose levels (massive hypoglycemia) that could directly endanger the patients’ life.

As DM is a widely researched area of biomedical engineering, almost every control method can be found in the literature. The most important directions focus on model predictive control” (MPC), fuzzy rule-based, classical PID control or robust control techniques; however, without having yet a general solution on the problem [19-21]. Simplistically, every control algorithm considers similar principles; namely, the fulfillment of prescribed quality and quantity properties. The first attempts on this area were related to ”Proportional-Integral- Derivative (PID)” control being still the most widely used classical control technique in the industry. Although the basic concept of PID control is not too sophisticated, highly advanced solutions like robust PID [30,31] or switching PID [32] have been applied for the AP concept.

MPC techniques represent probably the mostly used advanced control method in the AP concept, but they suffer from intra- and inter-patient variability and external noises. MPC is a model based solution meaning that the controller tuning is based on the properties of a mathematical model (called nominal model). Nonetheless, MPC algorithms produce the best results in individual therapy with considering closely ideal conditions. Several, highly developed MPC based control solutions appeared in the recent years like Robust MPC (RMPC), Nonlinear MPC (NMPC), Robust, Nonlinear MPC (RNMPC), MPC with moving horizon [33-36].

Soft computing methodologies have been applied also several times in the AP concept, but only in the recent years have been investigated in clinical trials [37-39]. Modern robust control methods like L2- or H∞-based ones were introduced in the AP researches in order to stave off the determinative uncertainties coming from inter- and intra patient variability. Supplemented by Linear Parameter Variability (LPV) methodology (providing the opportunity to handle the original nonlinear system/model as a linear one; hence, to give access using the original nonlinear model for linear control methods enumerated above), modern robust control successfully deals with the quality and quantity requirements [40-43].

Another useful direction in this domain proved to be the combination of LPV methodologies with Linear Matrix Inequalities (LMI)-based one [44, 45]. Its newest direction is connected to Tensor Product (TP) transformations based LMI controller design that is not validated yet in AP, but it can be useful in control of physiological systems [46-48].

Dual hormone controllers consider beside the insulin the glucagon hormone as well; hence, it represents another conceptual control approach in AP researches [49]. Clinical trials also starred in this direction with encouraging results [50].

2.3 Evolution of modeling aspects of diabetes from control perspectives

Controller design applications require a valid mathematical description of the physiological process of glucose-insulin interaction reflected in a mathematical model. The main considerations in the modeling of DM respect to the AP concept are briefly summarized in this section.

Figure-2 emphasizes the key elements to be accounted during modeling and controller development. The modeling of diabetes started with patient models having today highly advanced models available [20].

figure 2
Figure 2: Summary of the modeling questions of the AP concept.

The directions in this sense can be structured in two parts: inpatient and outpatient therapies. The goals of such models are different, since the circumstances and the environment of the patient are different. The followings give a short review on the evolution of the modeling parts developed from control theoretical perspectives.

Inpatient therapies mostly connect to Intensive Care Unit (ICU), where the strategy is to use as simple patient models as possible. As the patient’s environment is controlled by qualified medical staff and exact protocols, precise glycemic control is possible with prediction of the future condition of the patient as well. In the outpatient concept the patient requires complementary aspects as well, since physiological considerations to be taken into account are more complex then the ICU case; hence, the main expectation from an AP is an efficient control of the glycemic level with uncertain or sometimes unknown/ unrecorded events from the patient.

As a result, in parallel with the patient models additional models were included in the modeling loop in order to give more precised and more realistic physiological (models of digestion, absorption, β-cell, etc.) and physical (models of devices, sensors, etc.) processes.

2.4 The minimal model

As previously mentioned, the first models in the field of AP researches were connected to individual patient models. Their most important example is the Minimal Model (MM) developed by Bergman et al. [51-54]. Several extension of the MM were born in the last decades, however, the key concept remained the same in every case. One of these is the following modification [19]:

Ḡ(t) = -(ρ1 + X(t))G(t) + ρ1GB + ρ(t)

X̄(t) = -ρ2X(t) + ρ3[I(t) - IB]

Ī(t) = γ (G(t)) - h)t - η[I(t) - IB] + u(t)

The model stands from two main parts: the first two equations describe the glucose disappearance, while the third one is for the insulin kinetics. The main idea behind is that the patient gets glucose through p(t) [mg/min] meal absorption rate and the other input is the external insulin injection, u(t) [mU/min]. After a meal the absorbed glucose gets into the blood stream; hence, the blood glucose (BG) level, G(t) [mg=dL] is increasing. If G(t) is different than the pancreatic target glycaemia h [mg=dL], then the β -cells injects insulin to the blood. However, in case of T1DM (γ = 0) where these cells were burned out, the only insulin source is the external injection, u(t) [mU=min]. The connection between glucose and insulin dynamics is the rate of glucose disappearance, X(t) [min-1], which is higher if the level of insulin is increasing. Over the year’s lot of patient models were derived from the MM.

2.5 The ICU models

The ICU models maintain the MM structure, but in a more sophisticated way. The state variables are usually kept in low level ranges while taking into account important kinematic (e.g. decay velocity, diffusion) and physiological (e.g. glucose production of the liver) issues. Important representatives of such kind of models are the Canter bury models [55-60]. However, other models appeared as well [21].

2.6 Outpatient models

The outpatient models developed for the AP concept consider several physiological constraints and effects: the insulin dependent glucose consumption of the tissues whom main energy source is the glucose like muscles; the insulin independent glucose consumption of the nervous system; continuous glucose production of the liver (via the glycogenesis-glycolysis); absorption, diffusion, clearance and decay of the insulin and glucose; the effects of the insulin, etc. Most of these AP models are valid for T1DM due to its general symptom, the total lack of internal insulin production, and operate with high number (6-10) of state variables. One widely used model family was developed by Padova- Virginia group [19,20,61,62]. Based on their researches they created an FDA-approved diabetes simulator as well [63]. Another highly developed solution was created at Cambridge, UK [64,65]. A more complex advanced patient model was published at the MIT Boston USA [66], with more than twenty state variables. Although these models are highly developed, they do not provide solutions to other types of diabetes.

2.7 Model extension to the type 2 diabetes case

Based on the diabetic status of the patient modeling and control considerations occurring in T1DM can be used in the therapy of T2DM patients as well. However, mathematical modeling of T2DM is not a trivial question, since the internal insulin production of the body should be taken into account. Furthermore, it is really hard to identify the diabetic status of the patient. Initially, the insulin production can be really high over years (to compensate the high BG level); nevertheless, with the progression of the disease the insulin production is decreasing and finally, cease with the burnout of the β - cells. Moreover, high inter- and intra-patient variability can be occurred in the amount of the produced insulin because of several environmental causes. Important issue represents the discontinuous secretion of insulin, having rather a pulsatile nature hard to model [67]. That is the reason why only in the recent years T2DM models appeared [45,68-70]. Double diabetic state and the pulsatile nature of internal insulin production was also successfully modeled [70]. The models can be even more precise if the β -cells are also taken into consideration [71].

2.8 Model extension to the type 2 diabetes case

Digestion and absorption models can be essential parts of a patient model as the effects caused by these physiological processes affect directly the variation of the BG level. Digestion models contain more details (i.e. more state variables, considered effects, etc.) as they should describe the whole nutrition procedure (from the meal boluses to the glucose absorption into the blood). Absorption models are simpler because they describe the way of the glucose from the gastrointestinal system into the blood. Usually these kinds of models are focusing only to the carbohydrate (CHO) intake. Highly advanced digestion model was developed by Andreassen et al. [72,73], considering not just the CHO, but also complex meal intakes. The model of De Gaetano et al. [74] and Dalla Man et al. [61,75,76] considered only the CHO intake; however, the model structures are easier to be connected to the AP models having high precision as well. 6) Sensor models: The subcutaneous glucose route and its dynamics represents an important question in the glucose modeling as well, since the commercially available CGMS devices measure interstitial fluid glucose level and use a mathematical model or algorithm to calculate the most likely BG level [77]. Usually the diffusion model is embedded into the patient model [61,64], but it can be placed into the sensor model as well [78,79]. Simple compartmental models are also useful for this aspect of the AP concept [80]. In most of the cases, noise and disturbance models are implemented directly in the above mentioned models. White noise is the basic noise type using with patient and sensor models, while the aging effects of enzymatic based sensors are always treated as disturbances. Finally, regarding validation and testing the importance of the feeding protocol should be emphasized. Due to the fact that the developed solutions should be tested in realistic circumstances, randomized feeding protocols are used. That means that the time frames, amounts and composition of the meal intakes vary during the simulation time.

3. Conclusion

Diabetes Mellitus is an incurable, but treatable disease. For diabetic patients AP could represent probably the most performant solution maintaining their condition in an automatically controlled way. The paper gave an overview of the AP concept, devices, models and the control engineering issues. The clinical trials started in the last years in the AP researches place the concept very close to market applicability and hence to a reality.

Acknowledgments

Levente Kov´acs is supported by the J´anos Bolyai Research Scholarship of the Hungarian Academy of Sciences. Gy¨orgy Eigner thankfully acknowledges the support of the Robotics Special College of the Obuda University. The research was also supported by the Research and Innovation Center of the Obuda University.


References

  1. D. Federation (2013) IDF Diabetes Atlas, 6th ed. Brussel, Belgium: International Diabetes Federation. View
  2. Fony´o A, Ligeti E (2008) Physiology (in Hungarian), 3rd ed. Budapest, Hungary: Medicina.
  3. American Diabetes Association (2011) Diagnosis and classification of diabetes mellitus, Diabetes Care. 34: S5-S10. View
  4. National Institute of Health and Care Execellence (2015) Type 1 diabetes in adults: diagnosis and management. London, UK: NICE. View
  5. Pollan M (2009) In Defense of Food: An Eater’s Manifesto. 1st ed. London, UK: Penguin Press. View
  6. National Collaborating Centre for Chronic Conditions (2014) Type 2 Diabetes. London, UK: Royal College of Physicians. View
  7. Tripathy B, Chandalia H, Das A, Rao P, Madhu S, et al. (2008) Robust Control and Linear Parameter Varying Approaches, Application to Vehicle Dynamics, 2nd ed. New Delhi, India: Jaypee Brothers Medical Publishers. View
  8. Cleland SJ, Fisher BM, Colhoun HM, Sattar N, Petrie JR (2013) Insulin resistance in type 1 diabetes: what is 'double diabetes' and what are the risks? Diabetologia 56: 1462-1470. View
  9. Libman IM, Becker DJ (2003) Coexistence of type 1 and type 2 diabetes mellitus: "double" diabetes? Pediatr Diabetes 4: 110-113. View
  10. Pozzilli P, Guglielmi C, Caprio S, Buzzetti R (2011) Obesity, autoimmunity, and double diabetes in youth. Diabetes Care 34 Suppl 2: S166-170. View
  11. Buchanan TA, Xiang A, Kjos SL, Watanabe R (2007) What is gestational diabetes? Diabetes Care 30 Suppl 2: S105-111. View
  12. Wong V (2014) Diagnosis of gestational diabetes mellitus: Where are we at?Int J Diabetes Clin Diagn 1: 104. View
  13. Wild S, Roglic G, Green A, Sicree R, King H (2004) Global prevalence of diabetes: estimates for the year 2000 and projections for 2030. Diabetes Care 27: 1047-1053. View
  14. Gerland P, Raftery AE, Sevcikova H, Li N, Gu D, et al. (2014) World population stabilization unlikely this century. Science 346: 234-237. View
  15. Farret, Lugo-Garcia L, Galtier F, Petit P (2005) Pharmacological interventions that directly stimulate or modulate insulin secretion from pancreatic beta-cell: implications for the treatment of type 2 diabetes. Fundam Clin Pharmacol 19: 647- 656. View
  16. ElEssawy B, Li XC (2015) Type 1 diabetes and T regulatory cells. Pharmacol Res 98: 22-30. View
  17. Potter KJ, Westwell-Roper CY, Klimek-Abercrombie AM, Warnock GL, Verchere CB (2014) Death and dysfunction of transplanted β-cells: lessons learned from type 2 diabetes? Diabetes 63: 12-19. View
  18. Robertson R, Davis C, Larsen J, Stratta R, Sutherland D (2000) Pancreas and islet transplantation for patients with diabetes mellitus (technical review). Diabetes Care 23: 112-116. View
  19. Chee F, Fernando T (2007) Closed-Loop Control of Blood Glucose. 1st ed. Berlin Germany: Springer-Verlag. View
  20. Cobelli C, Renard E, Kovatchev B (2011) Artificial pancreas: past, present, future. Diabetes 60: 2672-2682. View
  21. Shah VN, Shoskes A, Tawfik B, Garg SK (2014) Closed-loop system in the management of diabetes: past, present, and future. Diabetes Technol Ther 16: 477-490. View
  22. Al-Tabakha MM, Arida AI (2008) Recent challenges in insulin delivery systems: a review. Indian J Pharm Sci 70: 278-286. View
  23. Sherr J, Tamborlane W (2008) Past, present, and future if insulin pump therapy: A better shot at diabetes control. Mt Sinai J Med 75: 352-361. View
  24. Valla V (2010) Therapeutics of diabetes mellitus: focus on insulin analogues and insulin pumps. Exp Diabetes Res 2010: 178372. View
  25. Medtronic (2012) Mini Med R 530G System User Guide. Northridge, USA: Medtronic MiniMed. View
  26. Tandem (2012) t:slimR Insulin Pump User Guide. San Diego, USA: Tandem Diabetes Care. View
  27. Roche (2015) Accu-ChekR Combo Training Handbook. Basel Switzerland: Roche. View
  28. Eigner G, Sas P, Kov´acs L (2014) Continuous glucose monitoring systems in the service of artificial pancreas,in SACI 2014-IEEE 9th International Symposium on Applied Computational Intelligence and Informatics. A. Szak´al, Ed. IEEE Hungary Section- 117-122. View
  29. Mayo Clinic’s Research Magazine (2011) Can an ’artificial pancreas’ normalize type 1 diabetes? July 2011. View
  30. Kamath S (2013) Model based simulation for type 1 diabetes patients. Asian Am J Chem 1: 11-19. View
  31. Ramprasad Y, Rangaiah G, Lakshminarayanan S (2004) Robust pid controller for blood glucose regulation in type i diabetics. Ind Eng Chem Res 43: 8257-8268. View
  32. Marchetti G, Barolo M, Jovanovic L, Zisser H, Seborg DE (2008) An improved PID switching control strategy for type 1 diabetes. IEEE Trans Biomed Eng 55: 857-865. View
  33. Kirchsteiger H, del Re L (2013) Robust tube-based predictive control of blood glucose concentration in type 1 diabetes. in 2013 IEEE 52nd Annual Conference on Decision and Control (CDC). IEEE 2084-2089. View
  34. Maxime P, Gueguen H, Belmiloudi A (2013) A robust receding horizon control approach to artificial glucose control for type 1 diabetes. Nonlin Contr Sys 9:833-838. View
  35. Hovorka R, Canonico V, Chassin L, Haueter U, Massi-Benedetti M, et al. (2004) Nonlinear model predictive control of glucose concentration in subjects with type 1 diabetes. Physiol Meas 25: 905-920. View
  36. Kirchsteiger H, del Re L Nonlinear model predictive control with moving horizon state and disturbance estimation - application to the normalization of blood glucose in the critically ill. in Proceedings of the 17th World Congress The International Federation of Automatic Control. IFAC 17: 9069-9074. View
  37. Atlas E, Nimri R, Miller S, Grunberg EA, Phillip M (2010) MD-logic artificial pancreas system: a pilot study in adults with type 1 diabetes. Diabetes Care 33: 1072-1076. View
  38. Herrero P, Georgiou P, Oliver N, Johnston DG, Toumazou C (2012) A bio-inspired glucose controller based on pancreatic β -cell physiology. J Diabetes Scien Technol 6: 606-616. View
  39. Osgouie K, Azizi A (2010) Optimizing fuzzy logic controller for diabetes type i by genetic algorithm, in 2010 The 2nd International Conference on Computer and Automation Engineering (ICCAE). ICCAE 4-8. View
  40. Kov´acs L, Szalay P, Alm´assy Z, Barkai L (2013) Applicability results of a nonlinear model-based robust blood glucose control algorithm,J Diabetes Scien Technol 7: 708-716. View
  41. Kov´acs L, Szalay P, Beny´o B, Chase G Applicability results of a nonlinear model-based robust blood glucose control algorithm. J Diabetes Scien Technol 7: 708-716. View
  42. Kovács L, Benyó B, Bokor J, Benyó Z (2011) Induced Lâ‚‚-norm minimization of glucose-insulin system for Type I diabetic patients. Comput Methods Programs Biomed 102: 105-118. View
  43. Szalay P, Eigner G, Kozlovszky M, Rudas I, Kovacs L (2013) The significance of LPV modeling of a widely used T1DM model. Conf Proc IEEE Eng Med Biol Soc 2013: 3531-3534. View
  44. Szalay P, Eigner G, Kov´acs L (2014) Linear matrix inequality-based robust controller design for type-1 diabetes model. in IFAC 2014-19th World Congress of The International Federation of Automatic Control 9247-9252. View
  45. LatafaT P, Palumbo P, Pepe P, Kov´acs L, Panunzi S, et al. (2015) An lmibased controller for the glucose-insulin system. in 2015 European Control Conference (ECC). IFAC 7-12. View
  46. Takarics B, Baranyi P (2015) Tp model-based robust stabilization of the 3 degrees-of-freedom aeroelastic wing section. ACTA Polytech Hung 12: 209-228. View
  47. Takarics B, baranyi P (2015) Friction compensation in tp model form - aeroelastic wing as an example system. ACTA Polytech Hung 12: 127-145. View
  48. Galambos P, Kuti J, Baranyi P (2013) On the tensor product based qlpv modeling of bio-inspired dynamic processes. in 2013 IEEE 17th International Conference on Intelligent Engineering Systems (INES). IEEE Hungary Section 79-84. View
  49. B´atora V, T´arnik M, Murgas J, Schmidt S, Nogaard K, et al. (2015) Bihormonal control of blood glucose in people with type 1 diabetes. in 2015 European Control Conference (ECC). IFAC 25-30. View
  50. Gingras V, Rabasa-Lhoret R, Messier V, Ladouceur M, Legault L, et al. (2015) Efficacy of dual-hormone artificial pancreas to alleviate the carbohydrate-counting burden of type 1 diabetes: A randomized crossover trial. Diabetes Metab 3636. View
  51. Bergman RN, Urquhart J (1971) The pilot gland approach to the study of insulin secretory dynamics. Recent Prog Horm Res 27: 583-605 passim. View
  52. Bergman RN, Ider YZ, Bowden CR, Cobelli C (1979) Quantitative estimation of insulin sensitivity. Am J Physiol 236: E667-677. View
  53. Bergman RN, Phillips LS, Cobelli C (1981) Physiologic evaluation of factors controlling glucose tolerance in man: measurement of insulin sensitivity and beta-cell glucose sensitivity from the response to intravenous glucose. J Clin Invest 68: 1456-1467. View
  54. Toffolo G, Bergman R, Finegood D, Bowden C, Cobelli C (1980) Quantitative estimation of beta cell sensitivity to glucose in the intact organism - a minimal model of insulin kinetics in the dog. Diabetes 29: 979-990. View
  55. Wong X, Chase J, Shaw G, Hann C, Lin J, et al. (2005) Comparison of adaptive and sliding-scale glycaemic control in critical care and the impact of nutritional inputs. In 12th International Conference On Biomedical Engineering 4. View
  56. Wong X, Chase J, Shaw G, Hanna C, Lotz T, et al. (2006) Model predictive glycaemic regulation in critical illness using insulin and nutrition input: A pilot study. Med Eng Phys 28: 665-681.
  57. Pielmeier U, Andreassen S, Nielsen B, Chase J, et al. (2010) A simulation model of insulin saturation and glucose balance for glycaemic control in icu patients. Comput Methods Biomec 97: 211-2 22. View
  58. Chase JG, Suhaimi F, Penning S, Preiser JC, Le Compte AJ, et al. (2010) Validation of a model-based virtual trials method for tight glycemic control in intensive care. Biomed Eng Online 9: 84. View
  59. Dickson J, Hewett J, Gunn C, Lynn A, Shaw G, et al. (2013) On the problem of patient-specific endogenous glucose production in neonates on stochastic targeted glycemic control. J Diabetes Sci Technol 7: 913-927. View
  60. Stewart K, Pretty C, Tomlinson H, Fisk L, Shaw G,et al. (2015) Stochastic model predictive (stomp) glycaemic control for the intensive care unit: Development and virtual trial validation. Biomed Signal Proces 16: 61-67. View
  61. Dalla Man C, Rizza RA, Cobelli C (2006) Mixed meal simulation model of glucose-insulin system. Conf Proc IEEE Eng Med Biol Soc 1: 307-310. View
  62. Magni L, Raimondo DM, Bossi L, Man CD, De Nicolao G, et al. (2007) Model predictive control of type 1 diabetes: an in silico trial. J Diabetes Sci Technol 1: 804-812. View
  63. Man CD, Micheletto F, Lv D, Breton M, Kovatchev B, et al. (2014) The UVA/PADOVA Type 1 Diabetes Simulator: New Features. J Diabetes Sci Technol 8: 26-34. View
  64. Hovorka R, Canonico V, Chassin LJ, Haueter U, Massi-Benedetti M, et al. (2004) Nonlinear model predictive control of glucose concentration in subjects with type 1 diabetes. Physiol Meas 25: 905-920. View
  65. Wilinska M, Chassin L, Acerini C, Allen J, et al. (2010) Simulation environment to evaluate closed-loop insulin delivery systems in type 1 diabetes. J Diabetes Scien Technol 4: 132-144. View
  66. Sorensen J (1985) A physiological model of glucose metabolism in man and it use to design and access improved insulin therapies for diabetes. Ph.D. dissertation, Department of Chemical Engineering, Massachusetts Institute of Technology. View
  67. Skjaervold N, stling DO, Hjelme D, Spigset O, Lyng O, et al. (2013) Blood glucose control using a novel continuous blood glucose monitor and repetitive intravenous insulin boluses: Exploiting natural insulin pulsatility as a principle for a future artificial pancreas. Int J Endocrin 1-6. View
  68. De Gaetano A, Hardy T, Beck B, Abu-Raddad E, Palumbo P, et al. (2008) Mathematical models of diabetes progression. Am J Physiol Endocrinol Metab 295: E1462-1479. View
  69. Kong J, Kumar S, Palumbo P (2014) Dde models of the glucoseinsulin system: a useful tool for the artificial pancreas,in Proceedings in Mathematics and Statistics, G. Ajomne-Marsan and M. Delitala, Eds. Springer, 2014, ch. Managing Complexity, Reducing Perplexity in Biological Systems 109-117. View
  70. Zimei W (2013) Mathematical models with delays for glucose-insulin regulation and applications in artificial pancreas,Ph.D. dissertation, Doctor of Philosophy Department of Mechanical Engineering, National University of Singapore. View
  71. Palumbo P, Ditlevsen S, Bertuzzi A, De Gaetano A (2013) Mathematical modeling of the glucose-insulin system: a review. Math Biosci 244: 69-81. View
  72. Arleth T, Andreassen S, Orsini-Federici M, Timi A, Massi Benedetti M (2000) A model of glucose absorption from mixed meals,in Modelling and control in biomedical systems 2000 (including biological systems): a proceedings volume from the 4th IFAC Symposium, E. Carson and E. Salzsieder, Eds. Pergamon Press 307-312. View
  73. Arleth T, Andreassen S, Orsini-Federici M, Timi A () Optimisation of a model of glucose absorption from mixed meals. Alborg Uni 1-28.
  74. De Gaetano A, Panunzi S, Matone A, Samson A, Vrbikova J, et al. (2013) Routine ogtt: A robust model including incretin effect for precise identification of insulin sensitivity and secretion in a single individual PLoS ONE 8. View
  75. De Geatano A, Hardy T, Beck B, Abu-Raddad E, Palumbo P, et al. (2006) System model of oral glucose absorption: Validation on gold standard data. IEEE T Bio-Med Eng 53: 2472-2478. View
  76. Dalla Man C, Toffolo G, Basu R, Rizza RA, Cobelli C (2006) A model of glucose production during a meal. Conf Proc IEEE Eng Med Biol Soc 1: 5647-5650. View
  77. Eigner G, Kov´acs L (2014) Realization methods of continuous glucose monitoring systems. Scientific Bulletin of the Politechnica University of Timisoara, Romania. 59: 175-183. View
  78. Scuffi C, Lucarelli F, Valgimigli F (2012) Minimizing the impact of time lag variability on accuracy evaluation of continuous glucose monitoring systems. J Diabetes Scien Technol 6: 1383-1391. View
  79. Wang X, Mdingi C, DeHennis A, Colvin A (2012) Algorithm for an implantable fluorescence based glucose sensor. In 34th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. IEEE EMBS 3492-3495. View
  80. Schiavon M, Dalla Man C, Dube S, Slama M, Kudva YC, et al. (2015) Modeling Plasma-to-Interstitium Glucose Kinetics from Multitracer Plasma and Microdialysis Data. Diabetes Technol Ther 17: 825-831. View
Best viewed in Mozilla Firefox, Google Chrome, Safari, Above IE 9.0 version
Privacy Policy | Copyright & Permissions
Copyright © 2013-2024 Graphy Publications, All Rights Reserved.