1. Introduction
Springback is the phenomenon which occurs when the applied load is removed from a metal which had undergone bending or forming process. During this process, elastic recovery takes place in the metal leading to shape error at the final product of sheet metal forming processes. Springback takes place in many different forms such as torsion, bending, twisting, etc. and is known to have too many factors affecting it like blank holding force, punch velocity, lubricating condition, orientation, and temperature, etc. The design phase has to determine the optimal setting for the product. And these earlier mentioned factors have been identified during the product designing phase. Sheet thickness, elastic modulus; yield stress, work hardening exponent, and many other factors play a vital role in influencing springback phenomenon. The final shape of the formed part is seriously affected by springback phenomenon leading to failure of the forming process. It is proven that sheet metal thickness plays an important role on the springback, however one cannot restrict the thickness as it has its own applications. Mostly, trial and error method is the approach dealt for many years in forming industry to study the springback problem. Considering the production rate and production cost requirement, it is necessary to find a better approach which helps in better comprehension of such effect in order to avoid waste of time with tryout operation and expenses associated to part discharge. The most common metal forming process is bending which is widely used in various sheet metal products such as supermarket shelves, housing utensils, automobile panels, etc. [1,2]. Sheet metal bending process is one of the most widely used manufacturing process in industry. Springback is usually a primary issue encountered during most sheet metal bending processes. There have been many studies which investigates the springback effect on sheet by several factors such as temperature, gauge, force and orientation and also have described the experimental study for the springback effect on various sheet metals by means of an optimization of springback effective parameters [3].
This springback becomes the origin of the defect of dimensional accuracy in a product. Two methods have been approached for controlling the springback deviations. The first approach involves in mechanical methods for reduction of springback by increasing sheet tension during forming process. This method enables greater plastic zone during forming and less amount of springback occurs during unloading. Although this approach is more efficient in many forming processes, but increasing the tension of the sheet results in tearing of work piece. In the second method, the main purpose is to compensate springback error by changing or modifying the tool design, in a way that springback is reduced and the target shape is produced. In such methods, the amount of springback is considerably reduced but it involves in changing the die geometry by performing repeated trial and error approach which is a time consuming process [4].
Several researches have been carried out to investigate and attempt to obtain the basic understanding of the springback phenomenon using numerical as well as experimental methods. The drawback of the previous approaches is that the modeling cannot be done without considering some simplifying assumptions. Kriging as non-linear modeling technique are suitable for model-based supervision of uncertain systems. Kriging interpolation model can be developed by using the experimental or numerical data without having to make any simplifying assumption. Instead, it needs sufficient input data to obtain a response and interpolate the results and build the approximation model with help of the results. The optimum parameters can be determined using the approximation model built by kriging. This kriging interpolation method evaluates an objective function in design space at several points so as to gain a good approximation.
In this present paper, springback due to typical L-shaped bending was considered as the subject to be investigated. Kriging based interpolation method was employed to map the nonlinear relationship between springback and various process parameters. The springback process was modeled and analyzed by using the finite-element tool ABAQUS, so as to obtain the springback value for different process parameter as the input sample for building the meta-model. In order to minimize springback, the important material parameters and process parameters were chosen as design variable, the optimal design parameters were obtained by using the kriging approximate ability and the global optimization ability of evolutionary strategy. Thus, the accurately prediction and effectively manipulation of springback were realized.
2. Surrogate Model Technique
Optimization process usually requires a large number of potentially expensive simulations. Although, there are lot of advancements in computational hardware and algorithms, they have not lessen the complexity of the resulting computational work because of the ever increasing appetite for improved modeling of physical processes and more detailed optimization. In-order to reduce the computational cost, surrogate models are mostly used in place of the actual simulation models. These surrogate models are also known as meta-models for this reason. This surrogate-based design optimization begins with design of experiments process which involves in identifying the locations in the design space where simulations will be conducted. Response data are often obtained through numerical simulations are collected at these locations and one or more candidate surrogate models are fitted to the data. Finally, few candidate models are chosen from the calculated responses to facilitate the objective and constraint calculation during the optimization process. These candidate models are chosen at the points in design space where the actual response are not available.
2.1 Kriging Model
Kriging interpolation model is a most popular analysis technique used for computer experiments in-order to create cheap computer ‘‘meta-model’’ as a surrogate model for computationally expensive engineering simulations. It is named after a South African mining engineer named D.G. Krige who developed this technique while trying to improve the accuracy in predicting the ore reserves, In Kriging model, the response function y(t) is generally represented as:
where β is the constant, and z(t) follows Gaussian distribution whose
mean and variance are 0 and σ2 respectively. When
where
where the ns is the number of design variables which is 2 in this study. The unknown parameters θ1, and θ2 are obtained from equation 2. Where θi (i = 1, 2 . . . n) > 0, and the optimization algorithm is used to solve Eq. (5). [5,6].
2.2 B. Initial analysis of sheet metal bending
The finite element code ABAQUS was adopted to conduct all the simulations, and the L-bending process was assumed under the plane strain deformation. The sheet metal plastic properties are assumed to be isotropic, which was described by the von Mises yield function. The corresponding strain hardening law was used to represent the non-linear form using the following equation
where σy is yield stress, εeq is equivalent plastic strain, K is hardening modulus and n is strain hardening exponent.
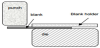
In this study, the sheet-metal was assumed to be too long and the L-bending could be simplified to a 2-D problem. The 2D model used for our analysis is depicted below in Figure 2 and the material properties are depicted above in Table 1. The sheet-metal was first between the blank-holder and the die surface and then the punch moved down to bend the sheet-metal into an L-shape. The tooling used in this bending process was modeled as rigid bodies, including punch, die and blank-holder while the blank is modeled as deformable body. Usually the 4-node plane-stress element was adopted for sheet metal to construct the mesh. The convergence test is generally performed to determine the number of elements to be used for the simulation along the thickness direction. Because the number of elements along the thickness direction has significant effect on improving the accuracy of the simulation. For our study, 6 layers of elements along the thickness direction were used. After the sheet-metal being bent into an L-shape, the punch and blank-holder were removed and the springback was calculated by determining the bent angle difference before and after the tooling was removed. Coulomb friction coefficient was utilized to describe the interaction between the tooling and sheet-blank during our simulation [7].
The numerical results of our analysis and the region where the springback takes place are depicted above in Figure 3. There are several factors such as the material performance, blank dimension and tool topological structure of sheet metals affect springback to some extent, but the influence degree is different. In-order to determine the most significant variable which has higher influence on springback, we performed the design of experiment using orthogonal array. On the basis of orthogonal analysis, the two most significant process parameters were considered here
- Punch radius
- Clearance gap along horizontal axis between the punch and the die.
These are the two factors that significantly affect the springback for our given data. So we have chosen these two variables as our design variable for our analysis.
3. Problem Formulation
3.1 Constructing objective function of optimization
Due to elastic deformation in the blank, there was some slight deviation in the blank between the component angle and tool angle after unloading which is termed as springback. The precision of the product and the subsequent assembly operations are affected severely due to the existence of springback. To compensate for the deviation caused by springback, a common method is to modify the forming process parameters. This is a challenging task and is largely performed by experienced designers using trial-and-error. In order to reduce manufacturing costs and improve the efficiency of design, this study use evolutionary strategy to optimize the process parameters in sheet metal forming. Thus the problem may be transformed into the problem of achieving the desired process parameters to minimizing springback value, which may be expressed as:
where F is the objective function, E1 and E2 are the design variables for the optimization problem. For our case, the objective is to minimize the springback angle (F) and the design variables are Punch radius (E1) and clearance gap between punch and die (E2). Also our problem is subjected to constraint which is the holder force to be lesser than 440 kN.
Because when the holder force is more than the given value, which may lead to local deformation and thinning problems on the blank. This value is chosen after experimenting with different holder force values through trial and error method as mentioned earlier.
3.2 Latin hypercube sampling
A great number of samples are generally required for computational algorithms in-order to achieve the accuracy. There are various techniques available to generate sample points to achieve this accuracy, but controlling the sample points is the key. Latin hypercube Sampling (LHS) is a widely used method to generate controlled random samples. This method operates by subdividing the sample space into smaller regions and sampling within these regions. The basic idea involved in this sampling technique is that the sampling point distribution is always maintained closer to the probability density function (PDF). The produced samples will more effectively fill the sample space and therefore reduce the variance of computed statistical estimators. This sampling method is highly effective compared to other sampling methods to achieve high accuracy and many studies have been carried out to test the efficiency of this sampling method. Stein M had research in the large sample properties of simulations using Latin hypercube sampling. Owen and Huntington tested the limitation of Latin Hypercube sampling [8,9]. Improved LHS have been developed, Stocki R projected samples onto a known subspace to minimize integrated mean square error and maximize entropy [10]. Iman had efforts to reduce spurious correlations, Florian rearranged the matrix of samples based on a transformation of the rank number matrix [11,12]. Further, methods for constructing orthogonal LHS are proposed to possess enhanced space filling properties, utilized iterative optimization methods are applied in LHS in order to reduce correlations. For our analysis we used MATLAB tool to generate this latin hypercube sample with help of MATLAB built-in command “lhsdesign”. Totally 30 sample points were generated for each design variable. This number is to be empirically determined from previous studies. For the first design variable (Punch radius), the lower and higher limits are 0.5 mm to 5 mm respectively. For the second design variable (clearance gap), the range is between 0 and 1 mm respectively. We chose this range in prior to our literature review and found that this range is suitably good for forming process for our given load and boundary conditions. Using the generated sample points, finite element analysis is carried out for each combinations in-order to extract the responses for the surrogate model.
4. Optimization Process
4.1 Building meta-model
The optimization problem for our case can be defines as
Minimize F(E1, E2)
subject to holder force ≤ 440 kN
the lower and upper limits for E1 are 0.5mm to 5mm and for E2 are 0 to 1mm respectively.
The meta-model was built using MATLAB which is tabulated
in Table 2. The column E1 and E2 represents the design variables
respectively,
4.2 Validation
The validation of kriging model was carried out using RMSE
(Root Mean Square Error) method. This validation process helps
to determine the genuinity of the surrogate model built. RMSE is
calculated between the actual response
where n is number of sample points and yi and
4.3 Optimization results
With help of genetic algorithm (GA) built in MATLAB, the optimization process has been carried out for the spring-back problem in bending process. Initially the kriging model for the response was generated based on those values and the parameter values for the kriging model for punch radius and the clearance gap were found to be 1.085 mm and 0.7354 mm respectively. After selection of optimum parameters, the finite element analysis is carried out for the given values and the optimal solution is determined to be 0.9943 which is depicted below.
| Response | True Value | Optimal solution |
| Spring Back Angle | 1.136 | 0.9943 |
Also it can be understood from the results that smaller punch radius and a smaller clearance gap helps in reducing the springback effect considerably.
5. Conclusion
In the present paper, a method for solving optimization problem based on kriging interpolation is presented, and is applied to optimize the sheet metal forming process. Based on finite-element analysis, the optimization of sheet metal forming process was accomplished by using the kriging approximate ability and the global optimization ability of evolutionary strategy for minimum springback. The process inputs were punch radius and clearance gap and main output was spring-back angle. The required validation data have been obtained from experimental observation. After development of predictive models, their performances were checked using root mean square error (RMSE). From the foregoing discussion, the following conclusions can be made:
- Kriging interpolation have the excellent ability of describing the high-nonlinear problems, like springback. The kriging model can be utilized for springback problems and it involves simpler steps to compute the problem.
- The ability of the prediction and optimization can be extended to consider an increased number of parameters and experimental results. Also, the variability of the experimental results affects the prediction and optimization performances.
- By using Kriging model, the spring back angle has been reduced by 12.47% for this simple 2D model and this value may vary for different model and the reduction percentage may increase drastically.
Competing Interests
The authors declare that they have no competing interests.