1. Introduction
Due to the importance of MHD generator power plant in power industry and its competition with gas turbine power plants, MHD power plant is worth studying. In fact MHD power plant is similar to the conventional Brayton cycle except in the latter a gas turbine is used instead of MHD generator. However the source for producing power is completely different.
In MHD power plant, as the working fluid which is a gaseous conductor passes through the generator in which there is a magnetic field, a current is generated. Hence the generator is a direct converter of electricity.
MHD generator is characterized by design simplicity, high operating temperatures as well as possibly high efficiency and absence of rotating parts which cause large centrifugal stresses as the case in gas turbines.
Regenerative Brayton cycle has been investigated with internally reversible [1] and internally irreversible conditions [2]. Recent mathematical models for MHD power plant with partial internal irreversibilities [3] and with variable temperature heat reservoirs [4] have been studied.
The maximum power output of MHD power cycle and the corresponding efficiency without considering the losses in the heat exchanger and in the compressor has been studied [5]. An analysis was carried out to find the maximum power density of MHD power cycle and the corresponding efficiency with considering the loss in the compressor but without considering the loss in the heat exchangers [6].
In the flow systems, thermodynamic irreversibility can be quantified through entropy analysis. Considerable research studies were carried out to examine entropy generation in the flow systems [7]. More research work regarding thermodynamic analysis of MHD an irreversible power plant with different operating conditions and with using regenerator in the power plant can be found in literature [8-11].
The objective of this paper is to investigate the generator effect on the cycle performance for constant velocity operating condition of MHD generator.
2. Analysis
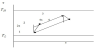
A MHD power plant consists of a compressor, heater, MHD generator and cooler. The T-s diagram of MHD power plant is illustrated in Figure 1.
The MHD power plant is running between an infinite heat source at temperature TH and infinite heat sink at temperature TL . Process 1-2 represents the nonisentropic compression, process 2-3 represents the isobaric heat addition in the hot side heat exchanger from an external heat source, process 3-4 represents the nonisentropic expansion process in the MHD generator, and process 4-1 represents the isobaric heat rejection in the cold side heat exchanger to an external heat sink. The isentropic processes 1-2s along the compressor and 3-4s along the MHD generator are also presented in Figure 1.
Considering counter flow heat exchangers, the rates of heat addition and heat rejection are, respectively,
where UHAH is the heat conductance on the hot side heat exchanger, ULAL heat conductance on the cold side heat exchanger (overall heat transfer coefficient -area product) and Cw capacity rate of the working fluid.
From Equations (1) and (2), we obtain
where εH and εL are, respectively, the effectivenesses of the hot side heat exchanger and cold side heat exchanger, for counter flow heat exchangers, they are given by [12].
The number of heat transfer units ΝH and ΝL are based on minimum heat capacity rates, which are defined
as
The power output and efficiency of MHD power plant are, respectively
Using Equations (1) and (3), and Equations (2) and (4), the following temperatures can be obtained as
The compressor efficiency is defined as
For the mathematical modelling of MHD power plant, we have assumed that the working fluid is a compressible ideal gas with constant specific heat, and all cycle processes are internally reversible except for the compressor and MHD generator. Using these assumptions and considering one dimensional steady state flow, the momentum and energy equations of the flowing gas in the MHD generator are written as, respectively,
where ρ is the gas density, u gas velocity, h gas enthalpy, p gas pressure , J current density, B magnetic field and E electric field.
The electrical efficiency of MHD generator is defined as [13]
Equations (11) and (14) give a clear idea about the internal irreversibilities of the compressor and generator, respectively. As the efficiencies of the compressor and generator approach 100 %, the MHD power plant is internally reversible but still externally reversible due to the finite heat transfer between the power plant and its thermal surroundings.
2.1 Constant velocity
In this case the flowing gas in the generator does not slow down but the electrical power comes from the work done by the expansion of the gases against the magnetic forces, i.e. from the enthalpy or thermal energy rather than the kinetic energy of gases.
Using Equations (12) - (14) gives
where k is the specific heat ratio of the working fluid. Equation (15) can be integrated for the process 3-4 to give
where the temperature ratio X is
By using Equations (7), (9) – (11) and (15) – (17), the power output
W can be written in terms of X only, and defining a dimensionless
power output as
The efficiency for constant gas velocity case can be expressed as
where
where γ is defined as
2.2 Efficiency at maximum power
The maximum dimensionless power outputs for constant velocity and constant Mach number can be found by maximizing Equations (18) with respect to X as
The solution of Equation (21) is too complex to obtain a simple analytical solution for the power output, hence a numerical solution is given in the next section.
For ηe = ηc = 1 and εH = εL, Equation (21) gives . For this special case the efficiency of MHD power plant at maximum power output is obtained as
which is known as Curzon and Ahlborn efficiency.
3. Results and Discussion
In this section, we present the results for constant velocity MHD
generator for k =1.4,
Figure 3 shows the variation of X with ηu. For ηe = ηc = 1 (endoreversible cycle), the efficiency of MHD power plant increases monotonically with X, however for ηe < 1 and ηc < 1, there exists a maximum. As can be seen from Figures 2 and 3, the maximum efficiency of MHD power plant occurs at higher X values than that of the maximum dimensionless power output.
One of the important points that worth mentioning is for ηe = ηc = 1 ,the working fluid has zero electrical resistivity and the constant velocity case is internally reversible by which it becomes identical to Joule-Brayton cycle. The results show that for ηe = ηc = 1, the cycle efficiency reached Carnot efficiency at X=5, for which the power output is zero, hence the cycle is internally and externally reversible, i.e. the heat engine is running at zero speed however the efficiency at X=1, is zero and hence zero power output, i.e. the heat engine is running at infinite speed.
4. Conclusions
An irreversible MHD power plant operating between an infinite heat source and heat sink has been analysed by using finite-time thermodynamics. The non-isentropic processes in the compressor and generator have been taken into account by introducing the compressor and generator efficiencies. The non-isentropic processes lower the power output as well as efficiency when compared with the endoreversible MHD power plant under the same operating conditions.
Competing Interests
The authors declare that they have no competing interests exits.