Profile

New User

New to Graphy Publications? Create an account to get started today.

Registered Users

Have an account? Sign in now.

How to Cite | Author Information | Publication History
International Journal of Earth & Environmental Sciences Volume 1 (2016), Article ID 1:IJEES-111, 11 pages
https://doi.org/10.15344/2456-351X/2016/111
Research Article
The Evolutionary Concepts and Practical Utilization of the T thian Theory of Regional Groundwater Flow

József Tóth

Department of Earth and Atmospheric Sciences, University of Alberta, Edmonton, Alberta, Canada
Dr. József Tóth, Department of Earth and Atmospheric Sciences, University of Alberta, Edmonton, Alberta, Canada, Tel: (780) 492-2178; E-mail: joe.toth@ualberta.ca
22 March 2016; 02 July 2016; 04 July 2016
Tóth J (2016) The Evolutionary Concepts and Practical Utilization of the Tóthian Theory of Regional Groundwater Flow. Int J Earth Environ Sci 1: 111. doi: https://doi.org/10.15344/2456-351X/2016/111
© 2016 Tóth et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Abstract

An attempt is made here to summarize the history and to highlight the major constituting concepts, properties and applications of the Tóthian Theory of Regional Groundwater Flow from its conception [1,2] to the mid 2010s.

Regional, or basinal, groundwater flow is defined here as “the gravity-driven cross-formational motion of groundwater at spatial and temporal scales that are commensurate with dimensions of the natural topographic relief and with the human and geologic time spans, respectively. The general “umbrella” theory is made up of two component sub-theories, namely: 1) "The Hydraulics of Basin-Scale Groundwater Flow" and 2) "The Geologic Agency of Basin-Scale Groundwater Flow".

The subject matter of “Sub-Theory-1” is the spatial pattern and dynamic intensity of groundwater flow in topographically defined drainage basins. This flow is organized into cross-formational flow systems driven by elevation differences in the water table through a hydraulically continuous rock framework. Owing to the flow domain’s hydraulic continuity flow systems develop ubiquitously and simultaneously throughout the entire porous portion of the Earth’s upper crust. “Sub-Theory-2”, on the other hand, deals with the processes, products and manifestations of the interaction between moving groundwater and its natural environment at and beneath the land surface.

The theory has resulted in a paradigm shift in hydrogeology. The paradigm of basinal groundwater hydraulics has changed from the classical perception of "confined, or artesian, aquifers" to the modern understanding of “regionally unconfined cross-formational flow systems". Or, in other words, form “pipe flow from outcrops to outcrops” in highly permeable strata between impermeable boundaries, to “regionally unconfined cross-formational flow systems" from recharge areas to discharge areas”. As a consequence, regional groundwater flow has been recognized as a unique and general geologic agent in the subsurface.


1. Introduction

Since it was proposed in 1962 as a simple analytical model of groundwater flow-distribution in a small drainage basin the model has evolved into the fully fledged Theory of Regional Groundwater Flow. It is an "umbrella theory” made up of two Sub-Theories: 1. The Hydraulics of Basin-Scale Groundwater Flow and 2. The Geologic Agency of Groundwater Flow. Sub-Theory-1 seeks to describe the distribution of gravity driven groundwater flow in drainage basins by means of mathematical models, field measurements of fluid dynamic parameters (hydraulic head, pore pressure, head- and/or pressure gradient, dynamic pressure-increment [3,4] and by observations of groundwater-flow related natural processes and phenomena. Sub- Theory-2 studies possible interactions between flowing groundwater, on the one hand, and its subsurface and surface environment, on the other (hydrological, chemical, thermal, mechanical, biological, etc.). Sub-Theory-1 is, therefore, the realm of the mathematician and engineer, while Sub-Theory-2 is home for specialists in a growing number of various disciplines dealing with groundwater related processes and manifestations. Normally, the two Sub-Theories attract students of different mentalities, backgrounds and interests. Yet the understanding and ability to exploit the full potential of the umbrella theory requires a familiarity with both of them.

The objective of the paper is, therefore, to present and explain the constituting principles, the principal attributes and the strongly interdisciplinary nature of the two Sub-Theories. The purpose, on the other hand, is to demonstrate how the groundwater-related interdependence and synergism between the two Sub-Theories can be used for the optimal application of the umbrella “Theory of Regional Groundwater Flow”. Simply put, to encourage, and pave the way for the interaction between specialists in either of the two Sub-Theories.

Note: It would be impossible pictorially to illustrate every significant aspect of a mature theory of broad scope in a single-paper essay on any of the natural sciences. The present study is no exception. This paper contains, therefore, only five fundamental figures that are, in the author's view, the most germane to the topic.

2. Regional Groundwater Flow Studies Prior to 1962

The idea that groundwater flow is induced by gravity goes back to times immemorial. Marcus Vitruvius Pollo [5] and Leonardo da Vinci [6] saw springs already as infiltrated rainwater, implying flow from higher to lower elevations; the artesian phenomenon was explained by Antonio Vallisnieri [7] by groundwater flowing in highly permeable geologic formations from elevated outcrops to low lying areas. But the question of a hydraulic structure, or patterns, of regional groundwater flow does not appear to have emerged until the late 19th and early 20th century. As it turns out, the universal control of that structure is the configuration of the water table.

An early, perhaps the first, purposeful and documented enquiry of the causal relationship between the water-table relief and the spatial distribution of groundwater motion was made by King [8,9] at the Wisconsin Agricultural Experiment Station Farm at Lake Mendota, Wisconsin, USA. A contour map of the water table based on 54 shallow observation wells over an area of approximately 370 m x 550 m adjacent to the lake was compared with the relief map of the land surface and the correlation was evident. Slichter [10] has envisioned “underground drainage basins” [10, p. 32] drawing a map of an undulating water-table with mounds and closed depressions and flow arrows pointing from high to low areas [10, Figure 9, p. 33]. Still in the same decade, D’Andrimont [11] (cited by [12, Figure 43, p. 87]) conceptualized a hierarchical pattern of groundwater flowdistribution consisting of a main drainage basin with one sub-basin on one side of the principal hill slope.

From the 1910s through the 1960s, inspired by Darcy’s [13] seminal paper [14-15], groundwater research was focused internationally on theories and empirical methods to predict well and aquifer yields (Note: not potential yields of extended areas or basins!) for steady state and transient conditions, in unconfined and confined aquifers and under different geologic configurations ([16-17]). The “era” of theoretical developments in aquifer and well hydraulics culminated in the concept of “leakage” (flow across slightly permeable strata sandwiched between more permeable ones) when applied to stacks of superimposed aquifers and aquitards [18-21].

Interest in basin-scale groundwater flow has re-emerged in the late 1950s and continued through the 1970s. The studies were empirical, based on field data (well-water levels, production tests, water chemistry) and conducted mainly for the purpose of municipal, industrial and agricultural water supplies [22-24]. The commonality in all those studies was the lack of a general and mathematically based theory. Each situation was thus treated as an individual case and interpreted according to the executor’s own ideas. In retrospect, many of the characteristics and controls of basinal groundwater flow glimmered through the results without, however, being recognized as such. Few investigations were dedicated specifically to the understanding of areal patterns of groundwater flow, their controls and consequences. And most of those which were [25-29], were also prompted explicitly by the theoretical developments of the early 1960s, to be discussed below.

3. The Theory of Regional Groundwater Flow

3.1 Sub-Theory-1: Theory of the hydraulics of basin-Scale flow systems

The opportunity of transition from speculative conceptualizations of basinal groundwater flow to quantitative analysis was provided by Hubbert's [30] seminal paper “The Theory of Ground-Water Motion”. Hubbert derived the basic fluid-dynamic parameter, Φ, mathematically from first principles and named it fluid potential and presented conceptual examples for its potential practical applications [30, Figs. 42, 45, 48].

Hubbert showed that the scalar quantity of fluid potential is the mechanical energy of a unit mass of water, ϕ, and it consists of two terms, one related to topographic elevation, z, the other to pore pressure, p:

Φ=gh=gz+ p ρ

where g is acceleration due to gravity, h is hydraulic head or the height of water column above the datum plane and ρ is the fluid’s density. Consequently,

−∇Φ=F

where F is the force driving a unit mass of fluid. Thus the force field can be calculated or modeled for any given flow domain along the boundaries of which ϕ or its first derivatives are stated. In turn, the flow field can be determined based on Darcy’s law [13] by combining the force field with the rock's hydraulic properties (porosity, permeability, storativity). Basinal-scale groundwater flow-patterns could now be produced mathematically as solutions to formal boundary value problems. Yet, another twenty years went by until this gift to hydrogeology was exploited.

3.1.1 Concept 1: The Unit Basin [1]

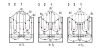
The first known application of Eq. 1 [30] to exploration for groundwater is attributed to Tóth’s papers of 1962a and 1963 [1,2]. The analytical study of basin-scale groundwater-flow patterns published in the first paper was prompted by an apparent discrepancy between observed stream flows in a number of creeks in the prairies of central Alberta, Canada, and those expected on the basis of Hubbert’s Figure 45 [30, p. 930]. Hubbert's figure shows that all the water that infiltrates over the entire surface of the basin returns along a line sink in the thalweg of the valley, as if the watercourse were a drainage ditch. In reality, however, the creeks beds were mostly dry. Based on "Figure 45", healthy runoffs in the creeks would be expected. On close scrutiny it appeared that the convergence of the figure’s flow lines was a postulate, not a result; Hubbert made the flow lines to converge on the thalweg, thus they did not necessarily simulate reality! The analytical solution of the first paper [1] to the Laplace equation for a basin of simple geometry and homogeneous geology provided the answer: all the water recharging the basin is not discharging into the one-dimensional line sink of the creek bed. Instead, it returns distributed over the entire lower half of the valley flanks leaving only a small portion to discharge in the thalweg. The flow pattern in the twodimensional section of a simple basin of quadrilateral shape, with two vertical and a horizontal impermeable boundaries, a linearly sloping water table and a homogenous-isotropic rock framework has come to be called with time "the Unit Basin" (Figure 1)[1, Figure 3, p. 4380] [32, p. 275, App. A].

figure 1
Figure 1: The Unit Basin ([[32 Figure 2.1, p. 27] modified from [1, Figs. 2 and 3, pp. 4379 and 4380]).

From this first, mathematically formulated, "Concept 1" the Theory of Regional Groundwater Flow has evolved through, up to now, eight subsequent and distinctly identifiable concepts, with progressively increasing in complexity. These concepts were: 2) Undulating upper boundary, "The Complex Basin" [2]; 3) Heterogeneous-anisotropic rock framework, arbitrary water-table relief [31,33,34]; 4) Regional hydraulic continuity ‒ Cross-formational flow ([35]; The concept leading to Sub-Theory-2); 5) Transient flow at geological time scales [36]; 6) Perpendicular flow system: 3-D basinal water balance/budgets [37]; 7) Effects of increasingly complex hydraulic properties of the rock framework on the Tóthian flow pattern (see references in the relevant section); 8) Intersystem hidden channels [38].

3.1.2 Concept 2: Undulating upper boundary, "The Complex Basin" [2]

It was clear during work on the first paper already [1], that the assumption of linearly sloping water table is only a first approximation of nature. The Laplace equation was solved again now for a drainage basin with a sinusoidal surface superimposed on the Unit Basin's linear regional slope as the top boundary of the flow domain, thus mimicking the water table of a rolling landscape (Figure 2) [39,2, Figure 3, p. 4807]. The analysis resulted in the basic model of groundwater flow for Composite Basins with a homogeneous and isotropic rock framework. The pattern comprises several flow systems of different order, namely local, intermediate and regional. Owing to their geometrical arrangement they were aptly called the "…hierarchically nested flow systems…" by Engelen and Jones [40, p. 9]. A flow system is called local if its recharge and discharge areas are contiguous; intermediate if its areas of recharge and discharge are separated by one or more local systems but are not located on the main divide and valley bottom; and regional if it links the basin’s principal watershed and thalweg hydraulically (Figure 2). These terms are considered relative and dependent of the scale of the area analyzed and the degree of resolution of the analysis.

figure 2
Figure 2: "The Tóthian Drainage Basin": Hierarchically nested gravity-flow systems of groundwater in drainage basin of homogeneous rock framework and complex topography. [2, Figure 3, p. 4807].
figure 3
Figure 3: Delayed adjustment of flow systems to changes in topography on geological time scales ([32, Figure 3.26, p. 78]; modified from [45, Figure 22, p. 498]).

Three novel concepts of fundamental consequences were advanced in the above papers: the “Unit Basin”, the “flow system” and "stagnation zones". These would prove to have tangible effects on the future direction and scope of evolution of the entire discipline of hydrogeology. One of such effect would be the recognition of flow systems as “subsurface conveyor belts”.

The significance of the Unit Basin is that its flow pattern comprises the three elemental regimes of basinal groundwater flow fields explicitly. It can thus be considered as the hydraulic unit in the structure of regional groundwater flow-patterns. These regimes are the: i) recharge or inflow, ii) transfer or throughflow, and iii) discharge or outflow. In a basin they are located, respectively, in the areas upslope, adjacent, and downslope relative to its hydraulic midline, which divides the recharge and discharge areas [32, Figure 2.1, p. 27].

The flow-system concept was proposed to identify rigorously distinguishable parts of regional groundwater flow fields. A flow system has been defined as “a family of flow lines connecting the whole or part of a recharge area with the whole or part of a discharge area” [32, p.252]. Similar to the Unit Basin’s basic pattern, each individual system has three identifiable segments also in a complex basin: recharge, throughflow, and discharge. However, as mentioned above, three general types of flow systems may be distinguished in the complex case: local, intermediate, and regional (Figure 2).

Stagnation zones are regions in the interior and/or along the boundaries inside a flow field where both the horizontal and vertical fluxes are near zero (zone) or zero (point). Such areas develop where flow systems moving in the same direction split or those moving in opposite direction meet. Such sites may function as subsurface accumulation of heat and matter and may heterogenize groundwater age-distribution in a basin.

3.2.3 Concept 3: Heterogeneous-anisotropic rock framework, arbitrary watertable relief [31,33,34]

The next major step in the theory's development was the publication of a sequel of three papers by Freeze and Witherspoon [31,33,34]. They have introduced numerical solutions to the Laplace Equation and analyzed flow patterns in basins of arbitrary topography and heterogeneous and anisotropic flow domain. These studies have evoked interest in the effect of the rock's properties on basinal flow patterns (e.g., [41]). In addition, the introduction of numerical methods has moved the theory from the stage of conceptualization into the realm of practical applicability.

In the second paper of the sequel Freeze and Witherspoon [33] explored the effects on basinal flow patterns of aquifers and aquitards stacked in two- and three-layer configurations, sloping aquifers outcropping in recharge and discharge areas, and lenses, or “partial layers”. Such effects can be quantified as differences between the fields of flow- and/or fluid-potential in the heterogeneous domains, on the one hand, as compared to those in homogeneous ones of identical boundary conditions, on the other. They can thus be identified and measured as “anomalies” of the potentiometric surface caused by introduction of the heterogeneities [32, p. 51-59].

In general, relatively highly permeable units (e.g., lenses, laterally extensive strata) tend to modify the surrounding flow- and potentialfields by funneling the flow lines into their upstream parts and diffuse them through the downstream end. The difference between the fluidpotential values in the homogeneous and the heterogeneous basin, i.e., the potentiometric anomaly, can be interpreted, just like some geophysical parameters, as an indicator of the type and nature of the heterogeneity. The potentiometric distortion effect of heterogeneities seems to stop once the ratio of aquifer-to-aquitard permeability exceeds 1000 [33] [32, p. 52]. This ratio was found to be a limiting value to increasing throughflow also in the case of lenticular rock bodies by Tóth [1, p.4384, Figure 8] and Tóth and Rakhit [42, p. 365, Figure 4]. Further details about the effects of various types of heterogeneities on regional flow patterns are given in Tóth [32, p. 50-70].

Two conclusions relevant to basin-scale groundwater flow patterns and affecting the further evolution of the theory have been drawn from the above studies:

  1. The effects of heterogeneities in the rock framework on a regional fluid-potential field are manifest as anomalies when compared to the potential field in a homogeneous basin with the same boundary conditions. These anomalies can be used to make quantitative inferences concerning the causative rock body (e.g., as to its quality as petroleum reservoir; [42]) and the regional flow field;
  2. Flow of water is possible even through the tightest appearing rock formation.

3.1.4 Concept 4: Regional hydraulic continuity ‒ Cross-formational flow [35]. (The concept leading to Sub-Theory-2)

The first theory of analyzing transient water levels during pumping tests was based on the assumption of "ideally confined" aquifers, in other words, that the confining aquitards are absolutely impermeable [16]. In rapid developments, however, the concept of leakage was proposed [18] which, by the early 1970s, was expanded to “multipleaquifer systems” [21]. In contrast, the question of cross-formational flow in basin-scale gravity systems had, apparently, not been broached until the studies of Tóth [3] and Tóth and Millar [36].

The conceptual similarities between leakage and cross-formational flow of the engineering and, respectively, natural sciences, as well as the mutually corroborative theories and observations, have lead to the hydrogeologist's formulation of the concept of hydraulic continuity of the rock framework. According to Tóth [43, 35, p. 4): “Regional hydraulic continuity is a phenomenological property of the rock framework. This property is quantified as the ratio of an induced change in pore pressure at a point of observation to an inducing change at a point of origin. A subsurface rock body is considered to be hydraulically continuous on a given time scale if a change in pressure at any of its points can cause a change at any other epoint, within a time interval measurable on the specified time scale. The hydraulically continuous behavior of the rock framework may be masked in large sedimentary basins by large distances, relatively short periods of observation, and sharp contrasts in flow-sensitive properties of subsurface fluids, such as temperature and chemical composition.”

3.1.5 Concept 5: Transient flow at geological time scales [36]

Some fundamental points of understanding have been distilled from the concept of basin-scale hydraulic continuity:

  1. Time is required for the fluid potential in any point of the flow domain to adjust, by diffusion, to changes in boundary conditions. Consequently, a modification in the relief of the water table results in transient differences between the actual, lagging field of fluid potential, on one hand, and the theoretical steady-state field that will ultimately develop and be adjusted to the new boundary, on the other. The length of the time lag is directly, while the size of the perturbation is inversely, proportional to the thickness and hydraulic resistivity of strata between the modified boundary and the point of observation.
  2. As a consequence of point i), several gravity-driven groundwater flow systems of greatly different temporal and spatial scales can coexist in a single flow domain as, e.g., a large drainage basin;
  3. Perturbation of the fluid potential field (or hydraulic head, pore pressure) in one flow system can propagate to other systems;
  4. Sharp contrasts in flow-sensitive fluid properties (temperature, chemical/isotopic composition, age mass) in a flow domain do not necessarily indicate permeability boundaries and/or absence of hydraulic communication.

Points i) and ii) are schematically illustrated in Figures 3a, b, c [44,32]. In the example the water table is assumed to coincide with the land surface on a basinal scale. Modification to the current topographic relief, S1, begins at time t1 (Figure 3a). S1 had been in existence for a sufficiently long time that the contemporaneous flow systems, q1, are adjusted to it and in steady state. At time t1 the land surface begins to change and by the time t1 the former upland S1 becomes the new valley S2 (Figure 3b). If the rate of topographic change is higher than the possible rate of cross-formational pressure-diffusion from the zone below the aquitard, a flow pattern develops which is incongruous with the relief. The now-modern flow systems, q2, in the high diffusivity upper parts of the basin follow the relief modification and remain adjusted to the upper boundary. The original q1 systems have been eliminated and become paleo, i.e., extinct, flow systems, q'1. However, due to the aquitard's low diffusivity, remnant differences in fluid potentials keep driving the gradually decaying relict systems, q1'', for a while in the lower portions of the flow region. Finally, at time t3 (Figure 3c), after sufficiently long time has elapsed for the relict potential differences in the aquitard to dissipate, the modern, steady-state systems, q3, are topographically adjusted and prevail throughout the entire basin; all previous flow systems have become extinct. They are, however, completely opposite in direction to what was their original orientation at time t1. In between, at time t2, the incongruous situation occurred that oppositely directed shallow and deep gravitational systems coexisted, with the deep systems flowing toward topographically high regions. In view of the possible wide range of adjustment times [36], such a puzzling situation appears to be entirely possible in a fluid regime which is hydraulically continuous and driven solely by gravity.

Conceptual illustration of delayed adjustment of flow systems to temporal changes in water-table relief: (a) original, t1, steady-state flow systems, monochronous flow field; (b) transient, t2, flow systems, heterochronous flow field; (c) final, t3, steady-state flow systems, monochronous flow field ([35, Figure 8, p. 12]; modified from [45, Figure22, p. 498]).

3.1.6 Concept 6: “Perpendicular flow system”: 3-D basinal water balance/ budgets [37]

Gleeson and Manning [37] approximated real-life simulation of basinal groundwater balances by introducing the "perpendicular flow system" oriented in the y direction, thus normal to the customarily used z-x vertical 2-D plane. The model domain covers an area of 6 km by 6 km. It was designed to simulate a network of three stepwise increasing mountain basins linked hydraulically by three mutually perpendicular river valleys. Each basin drains into the next, larger order stream: the small (first-order) into → the medium (secondorder) into → the large (third-order) stream [37, Figure 1]. The “perpendicular system" flows at right angles (in the y direction) to the primary or regional topographic gradient (i.e., parallel to the smallest or first order stream) from the divide of the second-order basin to the second order stream [37, Figure 1A].

The model was applied to three different types of mountain chains, namely, the: high relief (Himalayas), moderate relief (Rocky Mountains), and low relief (Appalachians) with respective topographic and recharge-rate parameters used. The study's objective was an analysis of sensitivity of the patterns and intensities of regionalscale groundwater flow systems in mountainous terrains to changes in topographic parameters and recharge rates. Two types of water-table configurations were considered: topography controlled and recharge controlled. In the first case, the water table is a subdued replica of the topography commonly found in humid climates and/or poorly permeable rocks. Recharge-controlled water tables occur, on the other hand, where recharge rates are lower than infiltration capacity as, for instance, in arid, rugged and high-permeability areas [46].

According to the study’s results the total rate of regional flow (flow parallel to the primary topographic gradient, i.e., to the second order stream) is always larger than that of the perpendicular flow. Nevertheless, the latter is “… a fundamental characteristic of mountain groundwater systems.” [37, p. 14] The primary factor controlling the relative rate of regional flow, as compared to the perpendicular flow, is the position of the water table. This, in turn, is governed by the ratio of recharge to hydraulic conductivity, R/K. Low water tables result in larger regional (potentially >60%) and smaller perpendicular flow components, while higher water tables induce relatively small regional flow (potentially near 0 %). The relation RL2/mKHd=1, proposed by Haitjema and Mitchell-Brooker [46] as a criterion for the transition between recharge-controlled (R<1) and topography-controlled (R>1) water tables, is supported by the study’s results. [In the relation R is areal recharge rate, K is hydraulic conductivity, L is the width of the principal drainage basin, H is average aquifer thickness, d is the maximum terrain rise, and m (dimensionless) is 8 or 16, depending on whether the problem is one-dimensional or radially symmetrical]. In cases of topography-controlled water table, regional flow depends mainly on the level of incision of the drainage network, as measured by the mean elevation of the first order stream relative to the mountain ridges, rather than on the ridges’ elevation.

An important aspect of the study is the conceptualization and quantitative definition of topographic and flow-system parameters required to characterize controls and properties of 3-D groundwater flow.

3.1.7 Concepts 7: Effects of increasingly complex hydraulic properties of the rock framework on the Tóthian flow pattern

Through the years of 2009-2011, eight mathematician hydrogeologists at several universities in China and the USA have co-authored, in various combinations, six papers examining by 2-D modeling the effects of increasingly complex configurations of the rock framework’s hydraulic conductivity, K, and porosity, Ѳ, on patterns, solute transport, water age and flushing intensity of gravitational groundwater flow-systems in “Tóthian type” drainage basins. The common starting points of the studies were the homogeneous and isotropic rock frameworks of Tóth’s “Unit Basin” (or "simple basin” [1,32] and/or composite flow domain [2] i.e., where hydraulic conductivity Kx=Kz=const and porosity Ѳ=const. The complexities were increased progressively through several cases: i) with depth, z, exponentially decaying isotropic conductivity, Kx(x,z)=Kz(x,z)=K0exp(Az), where K0= 1 m/d at the ground surface and A is the decay exponent with A=0 m¬-1 for the homogeneous case [47,48]; ii) with depth exponentially decaying K and Ѳ, where Kx(x,z)=Kz(x,z)=K0exp(Az) and Ѳ(x,z)= Ѳ0exp(A/n), n=2 being the porosity-decay exponent in Athy’s law [49-51]; iii) vertical downward increase and multi-scale anisotropy of K with different coefficients for “small-scale” (local) anisotropy aS=K0,x/ K0,z, “large-scale” (regional) anisotropy aL= Keq,x/Keq,z=aSaA, and aA=sinh2(Az0/2)/(Az0/2)2, which depends both on the depth of the basin and A as defined above [52]; and iv) to anisotropic permeability where kx/kz ≠ 1, and the horizontal and vertical components may decay at different rates with depth: kx = kx0exp(αz) and kz = kz0exp(βz), and: kx and kz are horizontal and vertical permeabilities [L2], respectively; -z is depth below land surface with +z being elevation (positive upward); kx0 and kz0 are the horizontal and vertical permeabilities on the ground surface [L2]; and α and β are the decay exponents for kx and kz, respectively [53].

The principal properties of flow fields that were explicitly and quantitatively analyzed as variables dependent on the structure of the rock framework include: i) the general characteristics of flow patterns, i.e., the type and geometry of the flow systems [47]; ii) the absolute and relative penetration depths of flow systems of different orders [47]; iii) areal distribution of recharge and discharge intensities [47]; iv) types, positions and rigorous definition of intra flow-system stagnation points and zones (singular points) of the flow fields [48]; v) rigorous delimitation of flow systems of different order [48]; vi) distribution of absolute and relative age of water in the Unit Basin and Tóth Basin [50]; vii) solute transport and residence-time distribution (RTD) in the Unit Basin and Tóth Basin, and their relevance for stream-bed and hyporheic conditions [51,52]; viii) “flushing intensity” and “flushing time” of flow in different parts and systems of the flow field [52]; ix) the shape of nested flow systems and the position, particularly the depth, of stagnation points between the flow systems as functions of the depth-dependent anisotropy ratio (kx/kz) [53].

3.1.8 Concept 8: Intersystem hidden channels [38]

The paper by Robinson and Love [38] is arguably the first and only one since Tóth [2] that has recognized a new elemental part in the hydraulic structure of the "Tóthian drainage basin", namely: the "hidden channels". These novel elements are narrow pathways of water flow which communicate between different orders of hierarchically nested groundwater flow-systems as defined by Tóth [2, p. 4798- 4806]. The channels convey water from recharge regions of a given order of flow systems into discharge areas of the next lower order system, e.g., from regional to intermediate or from intermediate to local systems thus they facilitate intersystem water exchange crossing apparent boundary lines between systems of different order. Those boundary lines had been considered earlier as separatrix stream functions linking corresponding stagnation points.

The "hidden channels" found by Robinson and Love (2013) are due to a slight asymmetry of the basinal flow pattern with respect to the vertical centerline of the rectangular flow domain. Although an asymmetry of flow- and fluid-potential distribution in the basin was noted earlier [2, p. 4808, point 3], its quantitative effects have remained undetected in the past because of the truncating errors of the calculation methods used. However, the combination of various analytical methods employed by the authors for locating stagnation points and specified streamlines results in solutions of higher resolution than those of earlier calculations.

The paper starts with a short review of numerous analyses and discussions of Tóth's [2] paper in the international literature with the justifiable purpose to stress the novelty and significance of the hidden channels' discovery.

Robinson and Love [38, Figure 1, Tables 1a and 1b] have studied a set of drainage basins identical to those of Tóth's [2, Figures 1, 2a- 2i] and presented analytical solutions for fluid potential, ϕ, stream functions, ψ, and horizontal and vertical velocities, vx, vz, respectively [38, Eqs. 9, 11 and 12].

In a separate section, stagnation points, where vx = vz = 0, and streamlines are considered. In a flow field whose pattern is ideally symmetrical with respect to the basin's vertical centerline the stagnation points occur where flow systems of different order converge or part. In such symmetrical cases, corresponding pairs of stagnation points upstream and downstream from the centerline develop between three lower order flow systems superimposed upon one higher order system in the latter's recharge and discharge areas [38, Figure 2].

As the study revealed, the stream-function values, Ψs, at corresponding stagnation-point pairs have fundamental structural significance for the basinal flow pattern. When these values are identical the two points can be joined by a single streamline of a specific stream function value. Such a streamline constitutes a noflow boundary between the neighboring flow systems and is called, therefore, a "separatrix": Ψs1 = Ψs2 (Figure 4a) [2, Figure 2f]; (Figure 4b) [38, Figure 5]. However, the regional decline in the fluid-potentials from the principal water divide towards the basin's main valley causes a slight asymmetry between the geometrical configuration of the uphill and downhill halves of the basinal flow pattern. This asymmetry results in differing stream function values at the two corresponding stagnation points: Ψs1 - Ψs2 = ΔΨs1-s2 ≠ 0. Each of the streamlines is joined, therefore, just to one of the two corresponding "upstream" and "downstream" stagnation points. In this scenario, and sufficient resolution of computation, no separatrix exists linking the two points (Figure 4c) [38, Figure 6]. Consequently, part of the water recharged in the higher order flow system (between the red-green and black-blue line pairs, Figs. 4b, c) will exit the domain in the discharge area of a lower order system. In other words, adjacent flow systems of different order will not be completely separated by a single line connecting the pair of upstream-downstream stagnation points.

figure 4
Figure 4: Flow net and separatrices in Tóthian drainage basin ([38, Figs. 2, 5, 6], respectively (a), (b) and (c) in present paper).

The two streamlines starting or ending at the corresponding stagnation points envelop an intersystem flow path, a hitherto unrecognized structural element of the basinal groundwater flow field, named by Robinson and Love [38] the "hidden channels".

(a): Gravity-driven pattern ([38, Figure 2] modified after [2, Figure 2f]). Dashed line: equal hydraulic head, solid line: stream line, full dot: stagnation point;

(b) Skeleton of flow pattern in Figure 4a calculated by low resolution computing [38, Figure 5]. Colored lines are separatrices, or boundary streamlines, between flow systems of different orders of magnitude (local, intermediate, regional). Blue and red separatrices connect corresponding stagnation points S1-S2 and S3-S4 in recharge and discharge areas seemingly preventing interflow between flow systems of different orders;

(c) Skeleton of flow pattern in Figure 4a calculated by high resolution computing and illustrating the channels by an exaggeration of 100. [38, Figure 6] Improved resolution of computation shows the effect of the regional slope of the water table.

Additional analyses in the paper have shown that knowledge of the stream-functions that bound a channel allows some conclusions also regarding their flow rates, width and the water's travel time. Such considerations are, however, beyond the scope of the present essay.

The theoretical significance of the “hidden channels” is fundamental. They are hitherto unrecognized structural elements of gravity-driven basinal groundwater flow. Their ability to conduct water from one type of flow system into another one, considered earlier to be hydraulically non-communicating, introduces a compelling new element into considerations of basinal water balances as well as groundwater flow as a geologic agent.

From a practical point of view and based on the sole study of Robinson and Love [38] the volumes of water moving through the channels appear to be negligible as compared to those moving through an entire basin or even to a single flow system. However, the calculations were done for homogeneous, isotropic, unstratified and unfaulted rock framework with a periodically undulating water table. Some modifications in the morphology and/or geology of the basin may cause significant changes in the flow pattern and strongly affect the size, shape and capacity of the channels. In turn, such changes in the channels can have unexpected effects on both the types and magnitudes of the geologic agency of basinal groundwater flow [54,32].

The three primary factors that have led to the development of the second component of the Theory of Regional Groundwater Flow were: i) Field studies dedicated to identifying manifestations of interaction between groundwater flow and the land surface soon after the theory’s proposal in 1963 [26,44,54,55,25,56,27,57,58]; ii) Numerical experiments of matter- and heat-transport [59,60] and iii) Recognition of the principle of regional hydraulic continuity [35].

The two fundamental causes for groundwater's active role in nature are: i) its ability to interact with the ambient environment in situ and ii) the organized spatial distribution of the products of interaction (heat, solutes, eroded particulate matter, and so on) transported by the flow systems acting as subsurface conveyor belts. Interaction and flow occur simultaneously and ubiquitously at all scales of space and time, albeit at correspondingly varying intensities at different localities. Thus, effects of groundwater flow are found from the land surface to the greatest depths of the porous parts of the Earth's crust, and from a day's length through geologic times. Three main types of interaction between groundwater and environment are identified in this paper, with several special processes for each one, namely: (1) Chemical interaction, with processes of dissolution, hydration, hydrolysis, oxidation-reduction, attack by acids, chemical precipitation, base exchange, sulfate reduction, concentration, and ultrafiltration or osmosis; (2) Physical interaction, with processes of lubrication and pore-pressure modification; and (3) Kinetic interaction, with the transport processes of water, aqueous and non-aqueous matter, particulates and heat. Owing to the transporting ability and spatial patterns of basinal flow, the effects of interaction are cumulative and distributed according to the geometries of the flow systems.

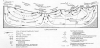
The number and diversity of natural phenomena that are generated by groundwater flow are almost unlimited. The abundance is due to the fact that the relatively few basic types are modified by some or all of the three components of the hydrogeologic environment: topography, geology, and climate. The six basic groups into which most manifestations of groundwater flow can be divided are: (1) Hydrology and hydraulics; (2) Chemistry and mineralogy; (3) Vegetation; (4) Soil- and rock-mechanics; (5) Geomorphology; and (6) Transport and accumulation [54]. Based on such a diversity of effects and manifestations, it is concluded that groundwater is a general geologic agent. A schematic diagram of processes, effects and manifestations are presented in Figure 5.

figure 5
Figure 5: Effects and manifestations of gravity driven flow in a regionally unconfined drainage basin ([54, Figure 1] modified from [61, Figure 10]).

4. Practical Applications of the Theory of Regional Groundwater Flow

It would be impossible to go into any meaningful detail about the actual and possible future applications of the Theory of Regional Groundwater Flow within the constraints of a single paper. Instead, a list of potential fields of application is provided below together with some appropriate references for readers of specific interests. A collection of examples can be found in Tóth [32], Ch. 5, “Practical applications: case studies and histories”, pp. 128-243.

  1. Interpretation of groundwater chemical/ionic composition [62,63,60,64].
  2. Saline soil genesis and amelioration [26,65,66].
  3. Conceptualization of surface water – groundwater interaction in different landscape environments [67].
  4. Groundwater resources [37,68-71].
  5. Genesis of and exploration for roll-front and tabular uranium deposits [72-74].
  6. Petroleum migration and accumulation [61,45,75-77].
  7. Soil mechanics [26,78].
  8. Rock mechanics [79,80].
  9. Heat transport ‒ Geothermics [59,81-84].
  10. Groundwater age dating (a warning about isotope interpretation! [50])
  11. Karst research [85-87].
  12. Nuclear fuel-waste disposal [88,89].
  13. Subsurface ecology [90].
  14. Satellite hydrogeology [91-93].

5. Conclusion

The intent of the paper is to present a concise but comprehensive overview of the evolutionary history, structure and possible applications of the Tóthian Theory of Regional Groundwater Flow. From a personal perspective it is the final work report on a lifetime scientific project.

Regional, or basinal, groundwater flow is defined here as “the gravity driven cross-formational motion of groundwater at spatial and temporal scales that are commensurate, respectively, with dimensions of the natural topographic relief and with the human and geologic time spans.” This umbrella theory comprises two sub-theories, namely: 1) "The Hydraulics of Basin-Scale Groundwater Flow and 2) "The Geologic Agency of Basin-Scale Groundwater Flow".

"Sub-Theory 1" deals with the spatial and temporal distribution of groundwater motion in natural drainage basins. It is based on the concept of the fluid potential, Φ, and its first version, the Unit basin, was proposed in 1962. The original concept has been refined by several major modifying attributes during the next five decades. Each of the modifications has increased the structural complexity of earlier basinal flow patterns, thus approaching reality progressively. In the meantime, the theory has caused a shift in the understanding of basinal groundwater hydraulics. The shift has occurred from the classical paradigm of "confined, or artesian, aquifers" (pipe flow from outcrops to outcrops in highly permeable strata) to the modern paradigm of “regional hydraulic continuity of the rock framework” (cross-formational flow systems from recharge areas to discharge areas). In other words, the modern paradigm is “cross-formational water flow in hierarchically nested patterns of regionally unconfined basin-scale systems".

Competing Interests

The author declare that there is no competing interests regarding the publication of this article.


References

  1. Tóth J (1962a) A theory of groundwater motion in small drainage basins in central Alberta, Canada. Journal of Geophysical Research 67: 4375-4387.
  2. Tóth J (1963) A theoretical analysis of groundwater flow in small drainage basins. Journal of Geophysical Research 68: 4795-4812. Reprinted In Physical Hydrogeology; Benchmark Papers in Geology, ed R. A. Freeze and W. Back (1983) Hutchinson Ross Publ. Co. Stroudsburg, Pennsylvania, U.S.A. p. 328-345.
  3. Tóth J (1978) Gravity-induced cross-formational flow of formation fluids, Red Earth Region, Alberta, Canada: analysis, patterns and evolution. Water Resources Research 14: 805-843.
  4. Tóth J (1979) Patterns of dynamic pressure-increment of formation fluid flow in large drainage basins, exemplified by the Red Earth region, Alberta, Canada. Bulletin of Canadian Petroleum Geology 27: 63-86.
  5. Pollo MV (1st c. BC) Reference to specific work is unavailable.
  6. da Vinci L (13th-14th c. AD) Reference to specific work is unavailable.
  7. Vallisnieri A (15th-16th c. AD) Reference to work is unavailable.
  8. King FH (1892) Observations and experiments on the fluctuations in the level and rate of movement of ground-water on the Wisconsin Agricultural Experiment Station farm and at Whitewater, Wisconsin: U.S. Weather Bureau Bulletin 5, 75 p.
  9. King FH (1899) Principles and conditions of the movement of ground water: U.S. Geological Survey 19th Annual Report, part 2, p. 59-294, accessed May 17, 2008.
  10. Slichter ChS (1902) The motions of underground waters. U.s.Geological Survey Water-Supply and Irrigation Paper, 67. Washington, DC: US Geological Survey.
  11. D’Andrimont R (1906) La Science Hydrologique (The Science of Hydrology) Revue Universelle de Mines. Liège, Bérange.
  12. Fourmarier P (1939) Hydrogéologie. Introduction à l’étude des eaux destinées à l’alimentation humaine et à l’industrie (Hydrogeology. Introduction to the study of water used for human consumption and by industry) Masson et Cie, Paris.
  13. Darcy H (1856) Les Fontaines Publiques de La Ville De Dijon. (The public fountains of the City of Dijon) Victor Dalmont, Paris.
  14. Dupuit J (1863) Études Théoriques et Pratiques sur le Mouvement des Eaux dans les Canaux Découverts et à Travers les Terrains Perméables (Theoretical and Practical Studies of Water Mouvement in Open Channels Permeable Rocks) Dunod, Paris, France.
  15. Thiem G (1906) Hydrogeologische Methoden (Hydrogeological Methods) Gebhart, Leipzig.
  16. Theis CV (1935) The relation between the lowering of the piezometric surface and the rate and duration of discharge of a well using groundwater storage. Transactions of the American Geophysical Union 2: 519-524.
  17. Walton WC (1960) Leaky Artesian Aquifer Conditions in Illinois. Illinois State Water Survey, Report of Investigations 39. Urbana, Illinois, U.S.A.
  18. Hantush MS, Jacob CE (1954) Plane potential flow of ground water with linear leakage. Transactions, American Geophysical Union 35: 917-936.
  19. Hantush MS, Jacob CE (1955) Nonsteady radial flow in an infinite leaky aquifer. Transactions, American Geophysical Union 36: 95-100.
  20. Witherspoon PA, Neuman SP (1967) Evaluating a slightly permeable caprock in aquifer gas storage: I. Caprock of infinite thickness. Journal of Petroleum Technology, pp. 949-955.
  21. Neuman SP, Witherspoon PA (1971) Transient flow of groundwater to wells in multiple-aquifer systems. In Aquitards in the Coastal Groundwater Basin of Oxnard Plain, Ventura County. Bulletin No. 63-4, Appendix A. Department of Water Resources, California, U.S.A. pp. 159-359.
  22. Geraghty JJ (1960) Movement of contaminants through geologic formations. 1990 Activities, National Water Well Association, Technical Division, Urbana, Illinois, U.S.A. pp. 33-43.
  23. Kolesov GD (1965) On the question of artesian feeding of rivers. Soviet Hydrology 3: 195-203.
  24. Albinet M, Cottez S (1969) Utilisation et interprétation des cartes de différences de pression entre nappes superposées (Utilization and interpretation of maps of pressure-difference between superjacent aquifers) Chronique d’Hydrogéologie de BRGM, Paris, 12: 43-48.
  25. Meyboom P, van Everdingen RO, Freeze RA (1966) Patterns of Groundwater Flow in Seven Discharge Areas in Saskatchewan and Manitoba. Geological Survey of Canada, Bulletin 147, Ottawa, Canada.
  26. Tóth J (1966a) Mapping and interpretation of field phenomena for groundwater reconnaissance in a prairie environment, Alberta, Canada. International Association of Scientific Hydrology Bulletin 16: 20-68.
  27. Mifflin D (1968) Delineation of Ground-Water Flow Systems in Nevada. Publication No. 4. Technical Report Series H-W, Center for Water Resources Research, Desert Research Institute, University of Nevada System, Reno, U.S.A.
  28. Hitchon B (1969) Fluid flow in western Canada sedimentary basin 1. Effect of topography. Water Resources Research 5: 186-195.
  29. Erdélyi M (1976) Outlines of the hydrodynamics and hydrochemistry of the Pannonian Basin. Acta Geologica Academiae Scientiarum Hungaricae 20: 287-309.
  30. Hubbert MK (1940) The theory of ground-water motion. The Journal of Geology 48: 785-944.
  31. Freeze RA, Witherspoon PA (1966) Theoretical analysis of regional groundwater flow: 1. Analytical and numerical solutions to the mathematical model. Water Resources Research 2: 641-656.
  32. Tóth J (2009) Gravitational systems of groundwater flow: Theory, Evaluation, Utilization. Cambridge University Press, Cambridge, UK. 297 p.
  33. Freeze RA, Witherspoon PA (1967) Theoretical analysis of regional groundwater flow. 2. Effect of water table configuration and subsurface permeability variation. Water Resources Research 3: 623-634.
  34. Freeze RA, Witherspoon, PA (1968) Theoretical analysis of the regional ground water flow. 3. Qantitative interpretations. Water Resources Research 4: 581-590.
  35. Tóth J (1995) Hydraulic continuity in large sedimentary basins. Hydrogeology Journal 3: 4-16.
  36. Tóth J, Millar RF (1983) Possible effects of erosional changes of the topographic relief on pore pressures at depth. Water Resources Research 19: 1585-1597.
  37. Gleeson T, Manning AH (2008) Regional groundwater flow in mountainous terrain: Three-dimensional simulations of topographic and hydrogeologic controls. Water Resources Research 44: W10403.
  38. Robinson NI, Love AJ (2013) Hidden channels of groundwater flow in Tóthian drainage basins. Advances in Water Resources 62: 71-78.
  39. Tóth J (1962b) A theoretical analysis of groundwater flow in small drainage basins. In Proceedings of Hydrology Symposium 3, Groundwater; October, 1962, Calgary. National Research Council of Canada, Associate Committee on Geodesy and Geophysics, Subcommittee on Hydrology. Ottawa, Canada. p. 75-106.
  40. Engelen GB, Jones GP ed (1986) Developments in the analysis of groundwater flow systems. IAHS publication 163, International Association of Hydrological Sciences. Wallingford, England.
  41. Kiraly L (1970) L’influence de l’hétérogénéité et de l’anisotropie de la perméabilité sur les systèmes d’écoulement (The influence of heterogeneity and anisotropy on [groundwater] flow systems) Bull. Ver Schweiz Petrol Geol Ing 37: 50-57.
  42. Tóth J, Rakhit K (1988) Exploration for reservoir quality rock bodies by mapping and simulation of potentiometric surface anomalies. Bulletin of Canadian Petroleum Geology 36: 362-378.
  43. Tóth J (1990) Hydraulic Continuity in Large Sedimentary Basins; Keynote Address, Proceedings of International Conference on Groundwater in Large Sedimentary Basins, Perth, Australia, July 8-10, 1990.
  44. Tóth J (1984) The role of regional gravity flow in the chemical and thermal evolution of ground water In Proceedings, Practical Applications of Ground Water Geochemistry, ed. B. Hitchon and E. I. Wallick. First Canadian/ American Conference on Hydrogeology, National Water Well Association and Alberta Research Council. Worthington, Ohio, U.S.A. pp. 3-39.
  45. Tóth J (1988) Ground water and hydrocarbon migration. In Hydrogeology. Geology of North America, v. O-2, ed. W. Back, J. S. Rosenshein and P. R. Seaber. Geological Society of America, Boulder, Colorado, pp. 485-502.
  46. Haitjema HM, Mitchell-Bruker S (2005) Are water tables a subdued replica of the topography? Ground Water 43:781-786.
  47. Jiang XW, Wan L, Wang XS, Ge S, Liu J (2009) Effect of exponential decay in hydraulic conductivity with depth on regional groundwater flow. Geophysical Research Letters 36: L24402.
  48. Jiang XW, Wang XS, Wan L, Ge S (2011) An analytical study on stagnation points in nested flow systems in basins with depth-decaying hydraulic conductivity. Water Resources Research 47: W01512.
  49. Athy LF (1930) Density, porosity, and compaction of sedimentary rocks. American Association of Petroleum Geologists Bulletin 14: 1-22.
  50. Jiang XW, Wan L, Cardenas MB, Ge S, Wang XS (2010) Simultaneous rejuvenation and aging of groundwater in basins due to depth-decaying conductivity and porosity. Geophysical Research Letters, 37: L05403,
  51. Cardenas BM, Jiang XW (2010) Groundwater flow, transport, and residence times through topography-driven basins with exponentially decreasing permeability and porosity. Water Resources Research 46: W11538.
  52. Zlotnik VA, Cardenas MB, Toundykov D (2010) Effects of multiscale anisotropy on basin and hyporheic groundwater flow. Ground Water 49: 576-583.
  53. Wang XS, Jiang SW, Wan L, Ge S, Li H (2011) A new analytical solution of topography-driven flow in a drainage basin with depth-dependent anisotropy of permeability. Water Resources Research 47: W09603.
  54. Tóth J (1999) Groundwater as a geologic agent: An overview of the causes, processes, and manifestations. Hydrogeology Journal, 7(1):1-14.
  55. Tóth J (2000) Las aguas subterráneas como agente geológico: causas, procesos y manifestaciones. Boletín Geologico y Minero, 111: 9-26
  56. Freeze RA (1969) Regional groundwater flow - Old Wives Lake Drainage Basin, Saskatchewan. Scientific Series No. 5. Inland Waters Branch, Dept of Energy, Mines and Resources, Ottawa, Canada.
  57. Williams RE (1968) Groundwater flow systems and related highway pavement failure in cold mountain valleys. Journal of Hydrology 6: 183-193.
  58. Williams RE (1970) Groundwater flow systems and accumulation of evaporate minerals. American Association of Petroleum Geologists Bulletin 54: 1290-1295.
  59. Domenico PA, Palciauskas VV (1973) Theoretical analysis of forced convective heat transfer in regional groundwater flow. Geological Society of America Bulletin 84: 3803-3814.
  60. Schwartz FW, Domenico PA (1973) Simulation of hydrochemical patterns in regional groundwater flow. Water Resources Research 9: 707-720.
  61. Tóth J (1980) Cross-formational gravity-flow of groundwater: A mechanism of the transport and accumulation of petroleum (the generalized hydraulic theory of petroleum migration) In Problems of Petroleum Migration, ed. W. H. Roberts III and R. J. Cordell. American Association of Petroleum Geologists, Studies in Geology 10: 121-167.
  62. Fritz P (1968) Osservacioni idrologiche sulle acque di Montecatini Terme (Hydrological observations on the thermal springs of Montecatini Terme). Bollettino di Geofisica Teorica ed Applicata 10: 15-27.
  63. Winter TC, Bidwell LE, Maclay RW (1970) Water Resources of the Wild Rice River Watershed, Northwestern Minnesota. Hydrologic Investigations, Atlas HA-339. U.S. Geological Survey, Washington, D.C., U.S.A.
  64. Engelen G B, Kloosterman FH (1996) Hydrological systems analysis: methods and applications. Kluwer Academic Publishers, Dordrecht Boston London.
  65. Macumber PG (1991) Interaction between Ground Water and Surface Systems in Northern Victoria. Department of Conservation and Environment, Victoria, Australia.
  66. Walker G, Gilfedder M, Evans R, Dyson Ph, Stauffacher M (2003) Groundwater Flow System Framework: Essential tools for planning salinity management. Murray-Darling Basin Commission, MDBC Publication 15/03. Canberra, Australia.
  67. Winter TC, Harvey JW, Fanke OL, Alley WM (1998) Ground Water and Surface Water − A Single Resouce. U.S. Geological Survey Circular 1139. Denver, Colorado, U.S.A.
  68. Tóth J (1966b) Groundwater Geology, Movement, Chemistry and Resources near Olds, Alberta. Bulletin 17, Research Council of Alberta. Edmonton, Alberta, Canada. Also: Alberta Geological Survey “Bulletin Series”, BUL-17) Edmonton, Alberta, Canada.
  69. Ortega GA, Farvolden RN (1989) Computer analysis of regional groundwater flow and boundary conditions in the basin of Mexico. Journal of Hydrology 110: 271-294.
  70. Delinom RM (2009) Structural geology controls on groundwater flow: Lembang Fault case study, West Java, Indonesia. Hydrogeology Journal 17: 1011-1023.
  71. Gleeson T, Befus KM, Jasechko S, Luijendijk E, Cardenas MB (2016) The global volume and distribution of modern groundwater. Nature Geoscience 9: 161-167.
  72. Galloway WE (1978) Uranium mineralization in a coastal-plain fluvial aquifer system: Catahoula Formation, Texas. Economic Geology 73: 1655- 1676.
  73. Garven G, Freeze RA (1984) Theoretical analysis of the role of groundwater flow in the genesis of stratabound ore deposits. 1. Mathematical and numerical model; 2.Quantitative results. American Journal of Science 284: 1085-1124.
  74. Sanford RF (1994) A quantitative model of ground-water flow during formation of tabular sandstone uranium deposits. Economic Geology 89: 341-360.
  75. Sanford R F (1995) Ground-water flow and migration of hydrocarbons to the Lower Permian White Rim sandstone, Tar Sand Triangle, Southeastern Utah. US Geological Survey Bulletin, 2000-J, Washington, DC.
  76. Verweij JM (1993) Hydrocarbon Migration System Analysis. Developments in Petroleum Science, 35. Elsevier.
  77. Verweij JM (2003) Fluid Flow Systems Analysis on Geological Timescales in Onshore and Offshore Netherlands – With Special Reference to the Broad Fourteens Basin. Netherlands Institute of Applied Geoscience TNONational Geological Survey, Utrecht, the Netherlands.
  78. Srisuk K, Archwichai L, Pholkern K, Saraphirom P (2015) Land use Changes due to Groundwater Exploitations at Ban Nong Khai Nun, Thaphra District, Khon Kaen, Northeast Thailand. GW-5, 5th GEOINDO 2015: 23-24.
  79. Iverson RM, Reid ME (1992) Gravity-driven groundwater flow and slope failure potential−1. Elastic effective-stress model. Water Resources Research 28: 925-938.
  80. Reid ME and Iverson RM (1992) Gravity-driven groundwater flow and slope failure potential−2. Effects of slope morphology, material properties, and hydraulic heterogeneity. Water Resources Research 28: 939-950.
  81. Bodmer Ph, Rybach L (1984a) Geothermal Map of Switzerland: Heat Flow Density. - Swiss Geophysical Comission, Zürich, Switzerland.
  82. Bodmer Ph, Rybach L (1984b) Heat flow maps and deep ground water circulation: Examples from Switzerland. - Journal of Geodynamics 4: 233- 245.
  83. Lazear GD (2006) Evidence for deep groundwater flow and convective heat transport in mountainous terrain, Delta County, Colorado. U.S.A.. Hydrogeology Journal 14: 1582-1598.
  84. Kooi H (2016) Groundwater flow as a cooling agent of the continental lithosphere. Nature Geoscience 9: 227-230.
  85. Klimchouk A (2007) Hypogene speleogenesis: Hydrogeological and morphogenetic perspective. National Cave and Karst Research Institute. Carlsbad, NM, U.S.A. Special Paper No. 1. 106 p.
  86. Goldscheider N, Mádl-Szőnyi J, Erőss A, Schill E (2010) Review: thermal water resources in carbonate rock aquifers. Hydrogeology Journal 18: 1303-1318.
  87. Mádl-Szőnyi J, Tóth Á (2015) Basin-scale conceptual groundwater flow model for an unconfined and confined thick carbonate region. Hydrogeology Journal 23: 1359-1380.
  88. Tóth J, Sheng G (1996) Enhancing safety of nuclear waste disposal by exploiting regional groundwater flow: The Recharge Area Concept. Hydrogeology Journal 4: 4-25.
  89. Voss C I, Provost AM (2001) Recharge-Area Nuclear Waste Repository in Southeastern Sweden − Demonstration of Hydrogeologic Siting Concepts and Techniques. Swedish Nuclear Power Inspectorate (SKI) Report 01:44. US Geological Survey, Reston, VA., U.S.A.
  90. Hancock PJ, Boulton AJ, Humphreys WF (2005) Aquifers and hyporheic zones: Towards an ecological understanding of groundwater. Hydrogeology Journal 13: 98-111.
  91. Bobba AG, Bukata RP, Jerome JH (1992) Digitally processed satellite data as a tool in detecting potential groundwater flow systems. Journal of Hydrology 131: 25-62.
  92. Hoffmann J (2005) The future of satellite remote sensing in hydrogeology. Hydrogeology Journal 13:247-250.
  93. Tweed SO, Leblanc M, Webb JA, Lubczynski MW (2007) Remote sensing and GIS for mapping groundwater recharge and discharge areas in salinity prone catchments, southeastern Australia. Hydrogeogy Journal 15: 75-69.
Best viewed in Mozilla Firefox, Google Chrome, Safari, Above IE 9.0 version
Privacy Policy | Copyright & Permissions
Copyright © 2013-2024 Graphy Publications, All Rights Reserved.