1. Introduction
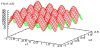
Many interesting problems in the literature have more than a locally optimal solution, leading to the possibility that there are multiple local or global optimums within the solutions search space. They are called multimodal problems [1]. In such problems, any kind of simple evolutionary algorithm can cause the convergence of the population to a restricted area of the search space, leaving the rest of local optimums. Usually, the standard genetic algorithms are not enabled for find the global maximum of a multimodal function [2]. In the resolution of this type of problems, normally it seeks to achieve several local or global optimums. In general, almost all search problems, formulated as an optimization problem, often has several maximums, where only one of them is better than the previous, which is defined as a global maximum. However, there are cases in which all global maximums have the same hierarchy, either because they have the same value or because a criterion for identifying which of them is better than the previous ones cannot be defined, as can be seen in the Figure 1.
This happens in the so-called multi-criteria or multi-objective optimization problems: in this case, the solutions are scored with regard to several variables or criteria where both have the same importance. For example, a typical transport problem is to define two basic criteria to complete a route passing through different established locations: 1) fuel spent and 2) time spent, where longer time for less fuel cannot be changed, and vice-versa, both are equally important. There will be better than other solutions, buy there will be cases where solutions cannot be compared (e.g. 12 liters and 90 minutes or 10 liters and 100 minutes). In these instances, a problem has multiple solutions consisting of all non-dominated solutions, i.e., those that define that there is no better solution than them. Genetic algorithms are prepared to solve this kind of problems. The multi-criteria optimization is defined as the problem of finding a vector of decision variables that satisfy some constraints and optimize a vector function whose elements representing the objective function.
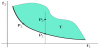
In accordance with the above deductions we can introduce Pareto optimality [3]. It is a concept of economy that has applications in engineering so it is a minimal notion of efficiency but not necessarily offer as results a desirable socially distribution of resources. Generally, the solution (in the Pareto sense, as we previously defined) to the problem of multi-criteria optimization does not need to be unique: the solution will be formed by the set of all vectors non-dominated, to which they are known by the name of non-dominated set or Pareto front. A solution x* is said to be Pareto-optimal if and only if no other vector that improves some of objectives exists, with regard to the values obtained by x*, without deteriorating simultaneously some of the others. In Figure 2, the Pareto front of a function with two objectives is shown in bold.
One solution to this type of problems it is to use multimodal evolutionary algorithms [2] based on preserving the population diversity using niches techniques [4]. This type of evolutionary algorithms are intended to divide the population into different niches so that solutions occupying different areas in the search space are able to survive to evolution, regardless of their quality, to reach different optimum of this kind of problems. In short, genetic algorithms evolve a population allowing solutions in different areas of solution space (niches).
Biological evolution provides a set of metaphors that act as inspiration when using genetic algorithms for solving multimodal problems. (1) Speciation or process by which different species can be adapted to occupy various ecological niches. The important feature is that species only reproduce with other member of the same species and therefore, existing mating restrictions. (2) Punctuated equilibrium is a theory which states that periods of evolution stagnation are interrupted by rapid growth when the principal population is invaded by individual within the group that had previously been isolated from the species itself. This process requires that the main population is separated in isolated subpopulations. (3) Local adaptation, this is the effect that occurs within a spatially distributed population when it is geographically separated into subpopulations of the same species and show adaptations to their local environment. Examples of this effect include birds or other animals developing eating habits which have a slightly different mouth in response to the presence of different types of food in different regions.
Based on these ideas, a set of mechanisms to help evolutionary algorithms in solving multimodal problems have been proposed, because generally evolutionary algorithms tend to converge around optimal due to the well-known genetic drift phenomenon [5]. To avoid premature convergence, two schemes are adopted in evolutionary algorithms: implicit and explicit. In explicit methods, specific changes in the population to preserve diversity are performed. In implicit methods, spatial distribution techniques are applied.
Within the explicit approach, we can classify them according to the formation of niches as spatial or temporal. Spatial methods allow formation of different niches in populations through the same run of a genetic algorithm. Temporal methods allow formation of different niches along different runs of a genetic algorithm. We will review in detail, in the next section, the different current applications of such methods in evolutionary processes: sharing, niching and crowding [4].
Up until this point, we have introduced a number of mechanisms that allow biological evolution to improve the evolutionary algorithms when facing multimodal problems. In section 2, the status of current approaches for solving multimodal problems in evolutionary algorithms is analyzed. Section 3 presents a critical opinion on the use of resolution mechanisms and finally, in section 4, the conclusions and future research are shown.
2. Methods
In this section, we review the range of options to find a variety of good solutions for multimodal problems avoiding premature convergence, from implicit approach, going through explicit solutions, to algorithms applied to multi-criteria optimization problem solving.
2.1 Implicit approach: spatial distribution
Implicit approach aims to use algorithms to divide the population into small subpopulations, giving a spatial distribution, such as the spatially structured Evolutionary Algorithms (ssEAs). The introduction of a spatial distribution in the population is justified by analogy with the effect of geographical separation in the evolution of biological individuals, which can help to improve the maintenance of diversity. These algorithms are called in various ways such as parallel or distributed evolutionary algorithms [6], also included within the ssEAs [7], noting the presence of a spatial structure as interaction graph.
In the literature, the most common models of ssEAs are the islands model [8] and cellular evolutionary algorithms [9]. The islands model [8] consists of multiple populations that run in parallel and there is a solutions exchange process between populations (called migration). The evolution algorithm applied and the initial population is the same for all nodes (islands). The only thing that changes are the individuals, it is like having multiple runs of the same problem in parallel. One of the most important ideas of this model is the migration or exchange of individuals between different runs on each node. This concept consists of swapping a small set of individuals of an island with other, depending on the structure that connects islands to one another. Using this method aims to achieve diversity in the islands, avoiding premature convergence of local minimum or maximum. These migrations are performed periodically and regularly. There are different topological models for interconnecting nodes or islands. This topology represents a directed graph. The most commonly used topologies are what can be seen in the Figure 3.
There are many studies on the effects of the different parameters for implementations of the islands model basic outline: degree of interconnection or islands network topology [10], periodicity migration [11], migrating individuals number [11] or the quality criteria for migrated individuals [11], but always it is concluded that solutions depend directly on the study problem.
Cellular evolutionary algorithms (cEAs) [9] structure population in small local areas, maintaining a population whose individuals are spatially distributed in cells. A cellular evolutionary algorithm is a genetic algorithm whose selection, recombination and mutation are performed within the neighborhood of each individual and finally, with a replacement strategy, it is decided whether the individual is substituted or not based on its offspring. The population can be updated through tow strategies: a synchronous strategy, where the entire population is replaced at the same time or an asynchronous strategy, where each individual is updated before moving to the next. This type of evolutionary algorithms, necessarily hold the diversity by the mating restriction (and the consequent material genetic exchange) through the physical distance between individuals.
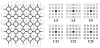
The population is usually structured in a two-dimensional grid (or mesh) of individuals as is shown in the left side of the Figure 4. Here, individuals (circles) located on the edge of the grid are connected to individuals who are ate the other edge of the grid in the same row and/ or column, as appropriate. The achieved effect is the one of a toroidal grid [12], so that all individuals have exactly the same number of neighbors. Normally, this type of evolutionary algorithms are defined in two dimensions (2-D) or square grid [13], but can also be defined other kind of topologies, or be extended to more dimensions.
The field of cellular evolutionary algorithms was very important with the emergence of massively parallel computers, but with the loss of popularity that this type of computers has suffered, the cEAs were partially forgotten by the scientific community. In recent years, thanks to the work of a few scientists aware of the parallel computing advantages, related works to solving complex problem through this technique on sequential machines have emerged gradually. Therefore, the cEAs are receiving increasing interest from the scientific community [14-16] and there are already many research groups that have an interest in this type of evolutionary algorithms [17]. One of the main features that bring about the cEAs good performance is the slow spread of the best solutions for the population, so the diversity of solutions between individuals is maintained longer with respect to other types of evolutionary algorithms.
The work carried out in the area in recent years is extensive and the effort to achieve a unified framework for categorize the different ways to apply parallel processing techniques to genetic algorithms (extrapolated to the rest to evolutionary algorithms) is manifest. In [18], a detailed overview of the parallel evolutionary algorithms can be reviewed. In this work, different approaches to the existing models of parallel evolutionary algorithms are detailed and referenced: slavemaster model, subpopulations with migration distributed model, overlapping static populations without migration models, massively parallel algorithms models and hybrid models.
2.2 Explicit approach
Multimodal problems began to be studied in the 80s. The general idea is to maintain the problem diversity so that when working with a group of solutions at the same time, different optimum of the problem could be obtained. Following this simple approach, many solutions have been proposed for solving multimodal problems.
One of the first approaches is the sharing systems. The classic method of sharing or sharing fitness [19] is based on the penalization of the search space areas with more solutions in the population. With this restriction, the solutions belonging to areas with high population density will reduce their quality compared to less populated areas. This is intended to ensure that sparsely populated areas are also explored. This is the reason why shared fitness is defined (following equation) and thereafter used in the selection process.
Where the original quality of the individual i is fi, the modified quality (sharing fitness) is and the modification function (sharing function) is Sh(d(i,j)). The modification function depends on the distance between individuals i and j (d(i,j)) according to the following equation:
Being σshare the radius that defines the belonging to two solutions to the same niche. The aim is to subdivide the search space into subregions or niches. To meet this goal, in the population and for each solution, only nearby solutions are sought (those that are closer than the defined radius (σshare)). If there are many solutions in a niche, it will be penalized against niches that have little or no solution, whose quality will be better and will be more likely to be analyzed in the search process.
The difficulty in maintaining diversity in this method caused that it was modified; giving rise to continuously updated sharing method [20]. The difference is that in this method, instead of penalizing the initial population areas of each generation, the population areas obtained during selection are penalized. With this modification, it seeks to penalize the areas in which several selected parents exist, limiting the possibility that its individuals are again chosen for the parent population.
Also based on the concept of niche (niching methods or niches algorithms), the clearing method uses the concept of limited resources to eliminate competition between solutions that are very different [21]. This method is based on the biological evolution of nature, in which only individuals of the same species fighting for the same resources available (and usually limited). Nevertheless, this struggle is not common among members of different species.
There are other niches algorithms methods. They are called crowding methods. Such algorithms form and maintain niches through the replacement of the population elements with similar individuals. They were studied intensively in [2] and they are based on each individual competes in a tournament with his parents, in such way that once selected a couple of parents and their descendants, tournaments for competing those closest individuals are done and they are selected for replacement. This approach has been called deterministic crowding. The deterministic crowding acts allowing the crossover of two individuals of different species. Children and parents are submitted to tournament, where a child will replace one of the parents only if it has better aptitude and belongs to the same class as its father.
In [4] and [22] a comparison of some methods applicable to evolutionary algorithms to improve the diversity in multimodal problems is done (sharing fitness, continuously updated sharing and deterministic crowding) and clearing that obtained the best result on examples of actual coding.
2.3 Multicriteria optimization
Historically there have been many approaches to solving problems of multicriteria optimization, from algebraic geometry applications [23] through heuristics [24] or by using evolutionary algorithms [25]. In this work, we focus only on the latter. One of the simplest solutions is to apply aggregative functions, i.e., a linear combination of different functions that need to be optimized, by assigning a weight to each. With this technique, it was possible to create an evaluation function that can be directly used in any selection method of evolutionary algorithms. However, it is not an efficient solution and does not always work properly. The definition of weights is subjective and this involves random results in domains of complex problems, being unable to generate all members of Pareto front if it happens it is concave.
An alternative approach is the so-called VEGA (Vector Evaluated Genetic Algorithm) proposed by Schaffer in the mid-80 [26]. Its operation is based on the division of the population in many subpopulations as different goals exist in optimization. Evolve certain location separately should be done, by looking only at one of the goals. After a time, populations are mixed and divided again. Thus, it was expected to obtain the Pareto front after a certain time. However, this option only works for compromises solutions, but fails to obtain the Pareto set. This situation ranks this approach within the techniques that do not meet the Pareto set. VEGA has been used in multiple works such as [27] or [28]. Moreover, there are other similar works that do not meet the Pareto set, such as lexicographical ordering or restrictions ɛ method.
From this point, subsequent algorithms and works take into account the concept of dominance or Pareto dominance. Applied to a minimization problem, the Pareto dominance can be defined as given a vector it is said that dominate another vector if and only if:
In addition, such solutions focus on obtaining the Pareto front explicitly. One of the first algorithms of this new approach can be MOGA (Multi-objective Genetic Algorithm) [29], where it is considered as individual fitness function to the inverse of the number of individuals in the population for which it is dominated. The fitness value obtained from an individual is linearized by mathematical interpolation algorithms, so that all individuals with a certain range have the same value for the fitness function. For that an uniform distribution occurs in Pareto front, sharing technique is used (defined above), applied to the actual values of the evaluation function. Its operation depends directly on sharing technique chosen and factor sharing used. Nevertheless, it has been used quite until a few years [30,31].
Other algorithms used today are the NSGA (Non-dominated Sorting Genetic Algorithm) [32], which use a division of the population in layers depending on their dominance and sharing for maintaining diversity. In addition, each layer receives a fitness which is proportional to population size. In terms of efficiency, this algorithm is less efficient than MOGA, so that it was optimized creating a review called NSGA II, where was added an elitism utilization and a comparison by crowding instead of sharing. It has been used in different works such as [33]. The NPGA algorithm (Niched Pareto Genetic Algorithm) employs a selection system using tournament based on Pareto dominance, but now instead of having only two individuals for comparison, uses up to 10% of the population for each comparison. In case of tie, sharing techniques are used to solve it.
Finally, one of the latest techniques is called SPEA (Strength Pareto Evolutionary Algorithm), which tries to integrate different techniques [34]. It uses a non-dominated solutions file and for each of them a force is calculated, which is similar to raking used by MOGA algorithm, i.e., proportional to the number of solutions that dominates. Also, it uses a clustering technique to maintain diversity. Two other current algorithms are an evolution of the SPEA technique: SPEA-2 and the PAES algorithm (Pareto Archiver Evolutionary Strategy).
In simple optimization problems with a single objective, methods that seek to maintain the explicit diversity, as we have detailed, are usually combined with implicit specialization methods which allow you to search the optimal solution within the niches (or subpopulations). By contrast, in the multi-criteria optimization problems, the goal of evolutionary algorithms for this approach is to try to distribute the population evenly along the approach to the Pareto front. Finally, we must emphasize that the most modern algorithms have left the exchange of fitness in favor of measures based on the distance, more akin to crowding.
3. Discussion
Judging from the current applications and theoretical developments reviewed, it seems clear that the population distribution and parallel evolutionary systems show an undeniable interest and provide multiple benefits. Structuring the population we can improve the numerical behavior of any kind of evolutionary algorithm, as well as to deal multimodal problems. However, it is difficult to extrapolate general conclusions about this type of models based only on existing jobs. This is because many of the existing studies are based on modified parallel models and away from the standards, or otherwise, they are tested on problems defined in the laboratory o they are problems which not represent reality.
In this section, we will conduct an objective review of the results obtained in the study of solving multimodal problems with evolutionary algorithms we have done.
Parallel evolutionary algorithms had a great boom with the appearance of massively parallel computers, and it would be normal that at present, with the existence of processing multiple cores on graphics cards for personal computers, they go back to the top of the evolutionary research. In such algorithms, as well as evolutionary computation in general, there are many open research lines, including the application of such algorithms to real complex problems. One of the main features that make this type of algorithms have a good performance is the slow diffusion of the best solutions through the population. This causes the diversity of solutions is maintained for longer than other types of evolutionary algorithms, allowing reaching multiple optimal. But in turn, it causes a slight disadvantage, increased in cellular evolutionary algorithms. It is a very slow convergence to the optimal, decreasing the algorithm efficiency. The problem today is only a slight handicap thanks to advances in parallel computing on GPU, and in contrast to parallel computers, the efficiency gains offset the problem of slow convergence. It would also be really interesting to evaluate such algorithms in large distributed computer networks (the load of every single process is simple and current communications through the Internet is very powerful). In this field, as we have seen, there are still many contributions that can be made.
Niches methods extent evolutionary algorithms to domains which require localization and maintenance of multiple solutions. We have found in the scientific literature that crowding methods are most effective against other types of niches methods. One of the critical issues in order to make this type of methods are functioning correctly and be really efficient is define correctly the replacement procedure or replacement selection. For example, in replacement parent techniques, the competition method between parents and children is crucial: many of the possible choices facilitate the algorithm obtained goes out of the niches methods, causing some instability in such methods, and that its use require a detailed study of the problem to be solved. Against this, the sharing method also includes some restrictions causing that it is used less and less efficient, as is the case of requiring a minimum population size for the method to have a high degree of success. Furthermore, it has been found that such methods require that algorithm parameterization is performed depending on the target searched and not just with the addressed problem information.
In some of the reviewed works, it has been found that the sharing methods are inefficient, not even operating for complex problems (current actual problems), while crowding methods (deterministic crowding mainly) can be applied to problems of any kind of complexity.
Evolutionary algorithms are one of the possible techniques for problem solving of multi-objective optimization or multi-criteria because as we have shown, they can simultaneously handle different sets of solutions (populations), see section above. This allows us to find several members of Pareto optimal set in only one algorithm execution. Also, it has been observed that evolutionary algorithms are less susceptible to Pareto front form or linearity (could be discontinuous or concave without difficulty) against other types of solutions for optimization problems of this kind. But the truth is that there are multiple techniques of evolutionary multi-criteria optimization as we have studied. Let us to review below a short evaluation of each of them. One to the simplest, as we seen, were the aggregate functions, using a linear combination of different functions with weights, but they have the great problem that does not work for problems which the Pareto front is concave as has been discussed in [35]. Proposed by Schaffer in the 80s [26], we have VEGA algorithms. They remain being efficient in computational terms and easy to implement, but maintain the same problem that aggregate functions in addition to their own problems. This is because if the proportional selection is used, then the merge of population subsets corresponds to the components average of the associated fitness with each of the objectives.
Faced with this type of solutions, techniques based on Pareto front appeared. They were proposed by Goldberg [36] and were based on the use of non-dominated sorting and selection to move the population towards the Pareto front. Among these techniques, we have studied several. MOGA maintains efficiency as the previous examples, but it grows in complexity when working with its computer implementation. Moreover, its performance depends directly on the proper selection of sharing factor used. Anyway, it is one of the most popular methods within this philosophy, especially for the control system design. NSGA by contrast is easier when it comes to implement, but suffers from the same handicap as the previous method, it seem very sensitive to the choice of sharing parameter values used. NSGA has been improved (NSGA-II) including elitism and a crowded comparison operator that maintains diversity without specifying any additional parameters, improving the original algorithm. The most efficient method evaluated in this work within this type of techniques has been NPGA. Its efficiency is due to the Pareto classification does not apply to entire population and further, it seems to have a good overall performance. In return, apart from needing the sharing factor parameter, it needs an additional adjustable parameter for the size of the selection by tournament, which detracts popularity.
The most recent approaches (last decade) as PAES or SPEA (and its evolution SPEA-2) are based on trying to minimize the appearance of new parameters for the control of evolutionary algorithm and maintain or improve the efficiency in favor of the search of the optimal solutions. From among all solutions studied, better yields, according to the literature, are obtained with evolved approaches NSGA-II and SPEA-2, where SPEA-2 improves its predecessors because performs better in complex search spaces, which gives it the advantage to perform better, in theory, on the real problems.
The main handicap for multi-criteria optimization problem solving is the solutions space size because the larger spaces (typical of the current real problems), the number of non-dominated solutions increases rapidly. This issue presents the greatest challenge to the use of multi-objective evolutionary algorithms techniques, i.e., maintaining the desired properties of convergence and simultaneously maintaining a good distribution of the solution space. This observation was the trigger or the main observation attaches great importance to the design model of the SPEA-2 approach. Although previous methods such as NSGA-II were faster in terms of complexity for the worst case, the question of density estimation becomes the most important objectives for complex problems.
Finally, as a final conclusion, it has proved necessary to study the dynamic behavior of the algorithms designed for each particular problem, as well as study the configuration parameters variation of the evolutionary algorithm to know the real behavior. Specifically, we can see data about the algorithm convergence speed or reveal devastating effects for efficiency as solutions premature convergence or else the possibility of stagnation occur, which cannot be evaluated from the static point of view of a theoretical study or either in a static state after an operating time.
4. Conclusions
In this work, we have done an introduction to evolutionary algorithms for solving multimodal problems and to the application of these techniques when it comes to solving multi-criteria optimization problems. This review begins by dividing the state of the art in three areas, approaches to parallel evolutionary algorithms, the extrinsic methods for solutions search spaces redistribution through niche techniques and current approaches to solving multi-criteria problems.
Almost all solutions for multi-criteria optimization problem solving use niches techniques that allow to evolutionary algorithms to locate and maintain multiple solutions within a population. For this reason, we have focused on activities related to this type of techniques, mainly in sharing and crowding models. Among the various methods used highlights the deterministic crowding because it is cheap computationally and further allows locating several optimal for a given problem, although the method of clearing, according to the studies reviewed, it is for the best results are obtained in general problems.
We have also seen some of the promising future task currently covered by evolutionary computation, among which stand out:
- Techniques that exploit parallel architectures: To delve into real problems exploiting current parallel architectures both at complete hardware machines level or graphics cards level.
- Self-adaptation: Avoid the use of ad-hoc parameters in the evolutionary algorithms.
- Better understanding the natural evolution: Computational simulations that help to understand the complex interactions that occur between living beings.
- Co-evolution: Many researchers have directed their efforts to study the co-evolution as an alternative model to the resolution of problems in evolutionary computation.
- The evolutionary algorithm without parameters: It is certainly the dream of all the experts, but today is a utopia.
As evolutionary algorithms are applied to search problems increasingly more large and complex, the design of faster algorithms that retain the ability to find acceptable solutions is necessary. In this work we have presented studies showing that parallel evolutionary algorithms are able to combine speed and efficiency, and that achieving a better understanding will allow us to use better them in the near future.
Competing Interests
The authors declare that they have no competing interests.