Profile

New User

New to Graphy Publications? Create an account to get started today.

Registered Users

Have an account? Sign in now.

How to Cite | Author Information | Publication History | Funding Information
International Journal of Computer & Software Engineering Volume 4 (2019), Article ID 4:IJCSE-142, 7 pages
https://doi.org/10.15344/2456-4451/2019/142
Research Article
Near Optimum User Selection for Minimum Mean Square Error Based Tomlinson Harashima Precoding

Satoshi Denno1*, Tomoyuki Baba1, Kenta Asaka2 and Yafei Hou1

1Graduate School of Natural Science and Technology, Okayama University, Okayama, Japan
2Department of the Engineering, Okayama University, Okayama, Japan
Prof. Satoshi Denno, Graduate School of Natural Science and Technology, Okayama University, Okayama, Japan; E-mail: denno@ec.okayama-u.ac.jp
27 December 2018; 29 January 2019; 31 January 2019
Denno S, Baba T, Asaka K, Hou Y (2019) Near Optimum User Selection for Minimum Mean Square Error Based Tomlinson Harashima Precoding. Int J Comput Softw Eng 4: 142. doi: https://doi.org/10.15344/2456-4451/2019/142
This work has been supported by JSPS KAKENHI Grant Number JP18K04142 and NTT DoCoMo, Co.Ltd.
© 2019 Denno et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Abstract

This paper proposes novel user selection techniques for the Tomlinson-Harashima precoding (THP) based on the minimum mean square error (MMSE) criterion. These techniques utilize a part of the intermediate values in the derivation of the THP weight, which makes it possible to implement the techniques with lower computational complexity. For further complexity reduction, we propose successive user selection techniques based on the techniques proposed above where user terminals are selected one by one. It is confirmed by computer simulations that the proposed techniques outperform conventional selection techniques. The computational complexity of the successive selection techniques is about 1/20 as small as that of the original selection techniques when 4 user terminals are selected out of 10 terminals.


1. Introduction

Wireless communication systems have been gradually evolved since the launch of the first generation digital wireless communication system. Network throughput of wireless communication systems has been raised along with the evolution. To provide users with high speed communication links, many techniques have been applied, for instance, adaptive modulation and coding (AMC), orthogonal frequency division multiplexing (OFDM), user scheduling, multiple input and multiple output (MIMO). Especially, MIMO is a key technology to increase the network throughput. MIMO techniques have been intensively investigated since the potential of MIMO was revealed [1]. While single user MIMO has been commercialized, multiuser MIMO has also been considered and been standardized in the IEEE 801.11ac, because multiuser MIMO can enhance network throughput in wireless communication systems only if many transmit antennas are put on a base station or an access point. Multiuser MIMO systems usually employ precoding in downlinks to order to avoid harmful interuser interference at user terminals. Precoding based on linear signal processing, so called “linear precoding”, has been proposed [2,3]. Besides, non-linear precoding has also been proposed [4-7]. Non-linear precoding attains better transmission performance than linear precoding [8], whereas non-linear precoding is more complicated than linear precoding. Although multiuser MIMO allows several user terminals to simultaneously communicate with an access point, the number of the accessible user terminals is limited. Multiuser MIMO has to select user terminals among all user terminals surrounding an access point. Because transmission performance greatly depends on channel condition between user terminals and an access point, user terminal selection techniques for linear precoding have been investigated [9-11]. User selection techniques for non-linear precoding such as Tomlinson-Harashima precoding (THP) [12-14] also have been investigated, because the THP can be implemented with relatively lower complexity than the other non-liner precoding. For example, user selection techniques to maximize throughput have been investigated [12,14]. Where the water filling is used in conjunction with the THP. Even when nonlinear precoding is utilized, a user selection technique for a linear precoding has been shown to be useful [13].

This paper proposes novel user selection techniques for the THP based on the minimum mean square error (MMSE) criterion with ordering. The THP based on the MMSE equalizes the signal to noise power ratio (SNR) of the received signals at all the user terminals. By taking advantage of the characteristic, the proposed user selection finds the a set of the user terminals that maximizes the SNR of all the received signals, which results in throughput enhancement. Because the proposed user selection techniques make use of an intermediate values in obtaining the precoder weights, the proposed user selection techniques only need a small amount of additional calculations. However, the proposed user terminal selection employs exhaustive search to find the best user terminal set. This paper proposes further low complexity user selection techniques that select user terminal successfully based on the user selection criterion used in the above proposed techniques, which mitigates the high computational complexity caused by the exhaustive search. Next section describes a system model, and the proposed user selection techniques are explained in Sec. III. Sec. IV evaluates the performance of the proposed techniques in terms of the transmission performance and the complexity. Concluding remarks are presented in Sec. V.

Throughout the paper, (A)-1, diag [V], superscript T, and superscript H denote an inverse matrix of a matrix A, a diagonal matrix with a vector V in the diagonal position, transpose, and Hermitian transpose of a matrix or a vector, respectively. tr [A] denotes a trace of a matrix A, i.e., a sum of the diagonal elements of the matrix A. E[β], ℜ [α] and 𝕴 [α] represent the ensemble average of a variable β, a real part and an imaginary part of a complex number α.

2. System Model

2.1 Multiuser Environment

We assume a wireless network where an access point with NAP antennas is surrounded by NU terminals. Only an antenna is placed on the terminal. The access point has packets to send to all the terminals. The channel state information (CSI) between the access point and all the user terminals is assumed to be known at the access point1. The access point sends the packets to the some user terminals simultaneously by utilizing MU-MIMO precoding, because MUMIMO precoding can prevent harmful multiuser interference from deteriorating the transmission performance at the user terminals. Let X ^ ∈ C N AP ×1 denote a transmission signal vector, a signal received at ith terminal, y(i) ε C, is written as follows.

1Access points are informed the CSI by explicit feedback in the uplink or implicit feedback in systems with time division duplexing.

y(i)= H i X ^ +n(i)

where H i ∈ C 1× N AP and ni ε C denote a channel vector between the access point and the ith terminal, and the additive white Gaussian noise (AWGN) at the ith terminal. Let Y∈ C N AP ×1 and N∈ C N AP ×1 denote a received signal vector containing the received signals at all the terminals and the AWGN vector consisting of the AWGN signals at all the terminals, they are defined as Y=(y(1)...y(NAP))T and N=(n(1)...n(NAP))T respectively. The received signal vector Y can be written as follows.

Y=H X ^ +N

where H denotes a composite channel matrix defined as,

H= ( H 1 T ... H N AP T ) T

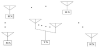
While the system model defined in (2) looks like only the NAP terminals receiving the signals, actually, the NU user terminals wait for the opportunity to receive the signals from the access point. Hence, NU >> NAP, This system model is illustrated in Figure 1. The access point has to select the |NAP user terminals among the NU user terminals. Because wireless channels are changed as time goes by, in principle, the selected user terminal set could be changed packet by packet. Because the signals are transmitted to only the users with which the THP achieves better performance, the average transmission performance of all the user terminals is expected to improve by the user terminal selection.

figure 1
Figure 1: System Model.

2.2 Tomlinson harashima precoding based on MMSE

It is demanded to provide user terminals with same quality services from the view point of fairness. In other words, the transmission performance should be equal among all the user terminals. For the purpose, we apply the THP based on the MMSE with the ordered Cholesky factorization [15]. When the THP is applied, the transmission signal vector X ^ is expressed as follows.

X ^ = g Ns F H V

In (4), F∈ C N AP × N AP and V∈ C N AP ×1 represent a feedforward filter weight, a feedback filter output signal vector, which are defined below. In addition, g N S ∈R represents a normalization factor defined as,

g N S = N S E[ | F H V | 2 ]

The feedback filter is obtained as follows. First of all, the error covariance matrix Φ is defined as,

Φ= ( H H H + γ N AP I ) −1

I∈ R N AP × N AP and γ ε R in (6) denote the identity matrix and a coefficient defined as γ N AP = N AP σ n 2 σ X 2 where σ n 2 and σ X 2 represent the power of the AWGN and that of the transmission signal vector X ^ . The error covariance matrix is Cholesky-factorized with ordering as follows.

PΦ P T = L H DL

P∈ C N AP × N AP ,L∈ C N AP × N AP  and D∈ C N AP × N AP in (7) represent a permutation matrix, a lower triangular matrix and a diagonal matrix. With the lower triangular matrix L, the ith feedback filter output signal v(i) ε C is obtained as follows.

B= L −1 −I

ν(i)=mod[ P i X− B i V, M d ]        = P i X− B i V+ k i M d    i=1... N AP

P i ∈ C 1× N AP ,B∈ C N AP × N AP , B i ∈ C 1× N AP ,X∈ C N AP ×1 , k i ∈C and Md ε R in the above equations represent the ith row of the permutation matrix P, an off-diagonal lower triangular matrix, the ith row of the off-diagonal triangular matrix B, a modulation signal vector, a Gaussian integer, a modulus used for a modulo function, respectively. The feedback filter output vector V is defined as V=(v(1)...v(NAP))T. Let c denote a complex number, in addition, mod [c,Md] represents a modulo function for a complex number, which is defined in the following.

mod[c, M d ]=M[ℜ[c], M d ]+jM[ℑ[c], M d ]

where j and M[a,Md] represent the imaginary unit and a modulo function for a real number defined as,

M[a, M d ]=a−⌊ a M d + 1 2 ⌋ M d

In the above equation, a ε R and ⌊ • ⌋ represent a real number and the floor function, respectively. Besides, the feed forward filter is defined with the matrices given by the Cholesky factorization as,

F H = H H P T L H D

Because the THP includes the modulo function, the THP is classified into non-linear precoding. The modulo function plays an important role in performance improvement of the THP. The modulo function makes user selection techniques for the THP differ from that for linear precoding.

In the following section, our proposed user selection techniques for the THP based on the MMSE with Cholesky factorization is described and the performances are compared.

3. User Selection for THP

We assume that n user terminals are selected among the NU user terminals. Since the number of the combinations is ( N U n ) the number of combinations grows very rapidly as the number of terminals NU increases. Let sn denote a set of selected user terminals where n represents the number of entries, kth entry in the set sn is denoted by ik (sn). Let a composite channel matrix between the select user terminals and the access point be represented as H S n , the composite channel matrix is defined in the following equation.

H S n = ( H i 1 ( S n ) T ... H i n ( S n ) T ) T

In the following, we describe user selection technique to choose the set sn to maximize the performance in terms of the transmission performance and the complexity.

3.1 Normalization factor based user selection (NUS)

When the signals are transmitted with the THP for the selected user terminals in the set S N AP , the received signal vector is rewritten as,

Y= H S N AP X ^ +N   ≈ g S N AP X+ M d K S N AP +N

In (14), K S N AP ∈ C N AP ×1 represents a Gaussian integer vector which is defied as K S N AP = ( k i 1 (S N AP ) ... k i N AP (S N AP ) ) T where k i m ( s N AP ) denotes a Gaussian integer generated by the feedback filter defined in (9) when the set S N AP is selected. Because the third term in the right hand side of (14) can be removed with the modulo function at the terminals, the transmission performance only depends on the amplitude of the received signal, i.e., g S N AP . Since the SNR of the received signals increases as the amplitude is raised, the transmission performance can be improved by selecting the set of the user terminals that maximizes the amplitude, which is defined as follows.

s ¯ N AP = arg max { i 1 ,... i N AP }∈ U N U [ g S N AP ]

where U N U represents a set including all the terminals as the entries. Because of the metric shown in (14), the user selection technique is called “Normalization Factor based User Selection (NUS)”. Because the user selection technique needs the precoder weights for all the possible combinations, big computational burden is imposed on the access point.

Low complexity user selection techniques are proposed in the following sections.

3.2 Diagonal matrix based user selection (DUS)

As is described in the previous section, the user terminal set that maximizes the amplitude g S N AP is regarded as nearoptimum set. As is defined in (5), the amplitude g S N AP depends on the power of the feedforward filter output vectors. The power can be rewritten as,

E[ | F S n H V S n | 2 ]=tr[ Ψ S n F S n H F S n ]

The matrix F S n in the above equation is the feedforward filter F defined in (12) when the set of the terminals, sn, is selected. The other matrices used in the THP are defined in the same manner, for instance, H S n , L S n , D S n , P S n , and  γ S n . Ψ S n in (16) denotes a covariance matrix of the feedback filter output vector V S n , which is defined as Ψ=E[ V S n V S n H ]=diag[ 1 σ V 2 ... σ V 2 ] where σ V 2 represents power of the feedback filter output signals coming out though the modulo function2. The matrix F S n H F S n can be further rewritten in the following equation after some mathematical manipulations.

2Power of the modulation signals is normalized to one. Because the first feedback filter output signal v(1) is identical to the input signal, the (1,1) entry of the matrix Φ S n is 1. On the other hand, the other output signals coming out though the modulo function are defined in (10). Hence, the other diagonal entries are reduced to σ V 2 that is different from the (1,1) entry.

F S n H F S n = H S n H P S n L S n H D S n ( H S n H P S n L S n H D S n ) H            = D S n − γ S n D S n L S n L S n H D S n

By substituting the matrix F S n H F S n in (17) for (16), the power of the feedforward filter output vectors can be rewritten as,

E[ | F S n H V S n | 2 ]= d S n (1)+ σ V 2 ∑ i=2 N S d S n (i)                      - γ S n tr[ Φ S n D S n L S n L S n H D S n ]

In (18), d S n (k) denotes the (k,k)-element of the diagonal matrix D S n . From the definition of γ S n , the last term in the right hand side of (18) is proportional to the AWGN power, which is expected not to be dominant in the power. We propose that the sum of the first and the second terms is used as a matrix to select the user terminals.

s ¯ N AP = arg min { i 1 ,... i N AP }∈ U N U [ d S N AP (1)+ σ V 2 ∑ i=2 N AP d S N AP (i) ]

The technique proposed in the section is called “Diagonal matrix based User Selection (DUS)”. Because it is unnecessary to obtain the normalization factor for all the possible combinations, the complexity of the DUS can be less than that of the NUS.

3.3 Correlation matrix based user selection (CUS)

As is shown in (9), the modulo function keeps the feedback filter output signal amplitude within half of the modulo Md. If the modulus Md is set to the infinity, however, the THP will be reduced to the linear MMSE precoding, and the power of the feedback filter output signals will be increased. Because the linear filter output vector X ^ S n can be written as X ^ = H S n H Φ S n X , the following inequality can be obtained from the relationship between the power of the THP and that of the linear precoding.

E=[ F S n V S n ]≤E[ | H S n H Φ S n X | 2 ]    ∼ σ 0 2 tr[ ( H S n H S n H + γ n I ) −1 ]

σ 0 2 in (20) represents the power of the modulation signals. In a wod, E[ X X H ]= σ 0 2 I since random bit sequence is assumed to be sent from the access point. If the linear MMSE filter can work similarly as the THP, we can expect that the power of the linear MMSE filter output signals can approximate that of the THP. Hence, we propose that the power of the linear MMSE filter output signals is used as a matrix to select the user terminals.

s ¯ N AP = arg min { i 1 ,... i N AP }∈ U N U [ tr[ ( H S N AP H S N AP H + γ S N AP I ) −1 ] ]

In the above, the power of the modulation signals σ 0 2 is omitted because the power is a constant and independent of the user selection. We call the user selection based on (21) as “Correlation matrix based User Selection (CUS)”. Since the CUS does not need Cholesky factorization, the computational complexity of the CUS can be reduced to less than that of the DUS.

3.4 Successive user selection

Although the reduced complexity user selection techniques, such as the DUS and the CUS, have been proposed, they require the exhaustive search to find the user terminal set. Because the number of the possible user terminal combinations is ( N U n ) as is described above, the complexity of those selection techniques grows in proportion to the number of the possible combinations.

In the section, we propose successive user selection techniques based on the user selection techniques proposed in the previous sections in order to reduce the complexity caused by the exhaustive search. The proposed successive user selection technique selects only the user terminal at once that maximizes the metric, which is repeated to find the NAP user terminals. Because only one user terminal is searched with the exhaustive search, the complexity of the selection is reduced to that proportional to N AP ( N U − 1 2 ( N AP −1) ) . The actual user selection techniques are written as follows.

3.4.1 Successive NUS (SNUS)

Successive user selection based on the NUS selects a user terminal based on the amplitude of the received signal. Let n - 1 terminals have been selected before by the technique, the selection technique find a user that satisfies the following equation.

i ¯ n = arg max { i n }∈ U N U −n+1 [ g { i n , S ¯ n−1 } ], S ¯ n ={ i ¯ n , S ¯ n−1 }

In (22), S ¯ n−1 and i ¯ n denote a set of the n-1 user terminals selected previously, and the selected user terminal index. As is shown in (22), only the i ¯ n th user terminal is selected, on the assumption that the user terminal set S ¯ n−1 has been selected as a subset of the optimum combination. In the lower equation in (22), the selected user terminal i ¯ n is added to the previously selected set S ¯ n−1 to form the updated set S ¯ n . This selection technique is named as “Successive NUS (SNUS)”.

3.4.2 Successive DUS (SDUS)

Similar to the SNUS, only the user terminal is selected that maximizes the metric used in the DUS as,

i ¯ n = arg max { i n }∈ U N S −n+1 [ d { i n , S ¯ n−1 } (1)+ σ V 2 ∑ i=2 n d { i n , S ¯ n−1 } (i) ] S ¯ n ={ i ¯ n , S ¯ n−1 }

This user terminal selection technique is called “Successive NUS”.

3.4.3 Successive CUS (SCUS)

A successive user selection technique based on CUS is also defined as follows.

i ¯ n = arg max { i n }∈ U N S −n+1 [ tr[ ( H { i n , S ¯ n−1 } H { i n , S ¯ n−1 } H + γ { i n , S ¯ n−1 } I ) −1 ] ] S ¯ n ={ i ¯ n , S ¯ n−1 }

This user terminal selection is called “Successive CUS (SCUS)”.

4. Computer Simulation

The performance of the proposed user selection techniques is evaluated in wireless multiuser communication environment drawn in Figure 1 by computer simulation. Rayleigh fading based on Jakes’ model is applied, because our proposed techniques are assume to be applied to mobile communication systems [16]. Modulation scheme is fixed to the quaternary phase shift keying (QPSK); " 1 2 (±1 ±j)" is sent as modulation signals from the access point. The modulus Md is set to 2 2 . Simulation parameters are listed in Table 1. The proposed techniques are compared with a conventional techniques, “Chordal Distance-Based User Selection (CDUS)” as a reference. Although the CDUS has been known to achieve superior performance in systems with linear precoding [17], we dare to compare our proposed techniques with CDUS, because some of our proposed selection techniques are also derived from the MMSE linear precoding.

table 1
Table 1: Simulation parameters.

4.1 BER Performance

Figure 2 compares the user selection techniques proposed in this paper with the CDUS in terms of the BER performance. In addition, the BER performance of the random selection is added as a reference. The number of the terminals is set to 10. Horizontal axis is Eb/N0. Although the CDUS achieves better performance than the random selection, the performance of the CDUS is about 4dB inferior to that of the NUS. The performance of the NUS is almost the same to that of the CUS and the DUS. Exactly speaking, the DUS achieves a little bit better performance than the NUS and the CUS, especially in the region of the BER less than 10-5.

figure 2
Figure 2: BER performance of original user terminal selection.

Figure 3 also shows the BER performance of the successive selection algorithms. The number of the user terminals is also 10. Similar as the performance shown in Figure 2, there is a big gap between the user selection techniques proposed in the paper and the others. However, the performance of the successive selection techniques is slightly degraded from that of their original techniques. For example, the performance of the SDUS is about 0.5dB worse than that of the DUS at the BER of 10-6.

figure 3
Figure 3: BER performance of successive user terminal selection.

4.2 Frequency utilization efficiency

The frequency utilization efficiency of the proposed user terminal selection techniques is evaluated with respect to the number of the terminals. Because the successive user terminal selection techniques achieve similar performance as their original selection techniques as is shown in Sec. IV-A, only the performance of the original selection techniques is shown in Figure 4, where the performance of the random selection and the CDUS are drawn for comparison. Eb/N0 is 6.64 dB. The performance of the random selection technique is independent of the number of the terminals. On the other hand, the performance of the other user terminal selection techniques is improved as the number of the terminals increases, because the probability that the user terminal sets are situated in more favourable conditions rises as the number of the terminals increases. As is shown in the figure, the frequency utilization efficiency of the DUS is much higher than that of the CDUS. This means that the DUS selects more favourable combinations than the CDUS, which agrees with the performance shown previously. The DUS achieves 160% higher utilization efficiency that the CDUS, and about 260% higher utilization efficiency that that of the random selection, when the number of the terminals is 10.

figure 4
Figure 4: Comparison downlink frequency utilization efficiency.

Figure 5 shows the frequency utilization efficiency of the DUS with respect to the number of the terminals. As is shown in this figure, the frequency utilization efficiency is rapidly saturated at 8 bit/Hz as the number of the user terminals increases, when Eb/N0 is high. When Eb/N0 is low, the frequency utilization efficiency is gradually going up as the number of the terminals increases.

figure 5
Figure 5: Frequency utilization efficiency of DUS.

4.3 Complexity

The complexity of the proposed user terminal selection is shown in Figure 6. While the horizontal axis means the number of the terminals, the vertical axis is the number of the complex multiplications performed per packet. The NUS has the higher computational complexity in spite of the number of the terminals. Though the complexity of the DUS and the CUS is less than that of the NUS, the complexity grows in parallel with the NUS, because the complexity of those two techniques is proportional to ( N U n ) . On the other hand, the complexity of the SDUS and the SCUS is much lower than the DUS and the CUS. The complexity of the SDUS is 1/20 as small as that of the DUS when the number of the terminals is 10.

figure 6
Figure 6: Complexity with respect to the number of terminals.

5. Conclusion

This paper has proposed novel user selection techniques for the Tomlinson-Harashima precoding based on the MMSE criterion with ordering. Those techniques are named NUS, DUS and CUS, respectively. While the NUS requires the THP weights for all the possible combinations of the user terminals to select the user terminals, the DUS and the CUS do not need the THP weights. Therefore, the DUS and the CUS can be implemented with less computational complexity than the NUS. Furthermore, this paper proposes further low complexity user terminal selection techniques that select the user terminals, successfully. The performance of the proposed user terminal selection techniques is evaluated by computer simulations. As a result, the DUS achieves slightly better BER performance than the others, and about 6dB better performance than the CDUS, a representative of conventional techniques. The SDUS is only 0.5 dB inferior to the DUS. However, the complexity of the SDUS is about 1/200 as small as that of the DUS.

6. Appendix A

6.1 Chordal Distance User Selection

Chordal distance user selection (CDUS) uses the chordal distance as a selection criterion [17], which is defined in the following equation.

d cd ( h C , H S )= 1−tr( h ^ C H ^ S H H ^ S h ^ C H )

In (25), h ^ C and H ^ S denote orothonormal matrices made from the hC and HS, respectively. The terminal that maximizes the chordal distance is selected in the CDUS technique, which is expressed in the following.

i ¯ n = arg max { i n }∈ U N S −n+1 [ d Cd ( h i n , H S ¯ n−1 ) ], S ¯ n ={ i ¯ n , S ¯ n−1 }

As is done in the proposed successive user selection techniques, the terminal that satisfies the above requirement is selected, and the user terminal index is added to the previously selected user terminal set.

Competing Interests

The authors declare that they have no competing interests.


References

  1. Foschini GJ (1996) Layered space-time architecture for wireless communication in a fading environment when using multi- element antennas. Bell Labs Tech J 1: 41-59. View
  2. Spencer QH, Swindlehurst AL, Haardt M (2004) Zero-forcing methods for downlink spatial multiplexing in multiuser MIMO channels. IEEE Trans Signal Processing 52: 461-471. View
  3. Spencer QH, Peel CB, Swindlehurst AL, Haardt M (2004) An introduction to the multi-user MIMO downlink. IEEE Commun Mag 42: 60-67. View
  4. Tomlinson M (1971) New automatic equaliser employing modulo arithmetic. Electronics Letters no 7: 138-139. View
  5. H Katsuda, Ohmori S, Akabane K (2016) Successive interference canceller with CSI weighting combining scheme. Proc. in the 84th Vehicular Technology Conference (VTC-Fall), Montreal, QC. View
  6. Harashima H, Miyakawa H (1972) Matched-transmission technique for channels with intersymbol interference. IEEE Trans Commun 20: 774-780. View
  7. Hochwald BM, Peel CB, Swindlehurst AL (2005) A Vector perturbation technique for near-capacity multi-antenna multiuser communication -Part II: Perturbation. IEEE Trans Commun 3: 537-544.
  8. Matsumoto T, Hatakawa Y, Kitagawa K, Konishi S (2013) Experimental results between non-linear and linear precoding using multiuser MIMO testbed. Proc Vehicular Technology Conference, Dresden. View
  9. Shi Z, Zhao C, Ding Z (2008) Low complexity eigenmode selection for MIMO broadcast systems with block diagonalization. Proc in IEEE Intern Conf Commun. View
  10. Shen Z, Chen R, Andrews JG, Heath RW, Evans BL, et al. (2006) Low complexity user selection algorithms for multiuser MIMO systems with block diagonalization. IEEE Trans Signal Processing 54: 3658-3663. View
  11. Kudo R, Takatori Y, Nishimori K, Ohta A, Kubota S, et al (2009) A new user selection measure in block diagonalization algorithm for multuser MIMO systems. IEICE Trans Commun 92: 3206-3218. View
  12. Demic G, Sidirompoulos ND (2005) On downlink beamforming with greedy user selection: Performance analysis and a simple new algorithm. IEEE Trans Signal Processing 53: 3857-3868. View
  13. Shimbo Y, Hiruma N, Maehara F (2018) Efficient combination of MUMIMO THP and user scheduling to achieve both high system capacity and fairness. IEICE Commun Express 7: 7-12. View
  14. Sun L, McKay MR (2014) Tomlinson-harashima precoding for multiuser MIMO systems with quantized CSI feedback and user scheduling. IEEE Trans Signal Processing 62: 4077-4090. View
  15. Kusume K, Joham M, Utschick W, Bauch G (2007) Cholesky factorization with symmetric permutation applied to detecting and precoding spatially multiplexed data streams. IEEE Trans Signal Processing 55: 3089-3103. View
  16. Jakes WC (994) Microwave mobile communications. IEEE Press. View
  17. Zhou B, Bai B, Li Y, Gu D, Luo Y, et al. (2011) Chordal distance-based user selection algorithm for the multiuser MIMO downlink with perfect or partial CSIT. IEEE International Conference on Advanced Information Networking and Applications, Biopolis Singapore. View
Best viewed in Mozilla Firefox, Google Chrome, Safari, Above IE 9.0 version
Privacy Policy | Copyright & Permissions
Copyright © 2013-2024 Graphy Publications, All Rights Reserved.